题目内容
【题目】如图，点P在射线AB的上方，且∠PAB=45°，PA=2，点M是射线AB上的动点(点M不与点A重合)，现将点P绕点A按顺时针方向旋转60°到点Q，将点M绕点P按逆时针方向旋转60°到点N，连接AQ，PM，PN，作直线QN.
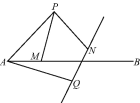
(1)求证:AM=QN.
(2)直线QN与以点P为圆心，以PN的长为半径的圆是否存在相切的情况?若存在，请求出此时AM的长，若不存在，请说明理由.
(3)当以点P为圆心，以PN的长为半径的圆经过点Q时，直接写出劣弧NQ与两条半径所围成的扇形的面积.
【答案】(1)证明见解析； (2)存在.理由见解析； (3)劣弧NQ与两条半径所围成的扇形的面积为π.
【解析】
（1）根据旋转的旋转判断出△APQ为等边三角形，再判断出∠APM=∠QPN，从而得出△APM≌△QPN即可；
（2）由直线和圆相切得出∠AMP=∠QNP=90°，再用勾股定理即可求出结论；
（3）先判断出PA=PQ，再判断出PQ=PN=PM，进而求出∠QPM=30°，即可求出∠QPN=90°，最后用扇形的面积公式即可．
(1)如图1,连接PQ,由点P绕点A按顺时针方向旋转60°到点Q,
可得AP=AQ,∠PAQ=60°,
∴△APQ为等边三角形,
∴PA=PQ,∠APQ=60°,
由点M绕点P按逆时针方向旋转60°到点N,
可得PM=PN,∠MPN=60°,
∴∠APM=∠QPN,则△APM≌△QPN(SAS),
∴AM=QN.
(2)存在.理由如下:
如图2,由(1)中的证明可知△APM≌△QPN,
∴∠AMP=∠QNP,
∵直线QN与以点P为圆心,以PN的长为半径的圆相切,
∴∠AMP=∠QNP=90°,即PN⊥QN.
在Rt△APM中,∠PAB=45°,PA=2,
∴AM=
.
(3)由(1)知△APQ是等边三角形,
∴PA=PQ,∠APQ=60°.
∵以点P为圆心,以PN的长为半径的圆经过点Q,
∴PN=PQ=PA.
∵PM=PN,
∴PA=PM,
∵∠PAB=45°,
∴∠APM=90°,
∴∠MPQ=∠APM-∠APQ=30°.
∵∠MPN=60°,
∴∠QPN=90°,
∴劣弧NQ与两条半径所围成的扇形的面积是扇形QPN的面积,而此扇形的圆心角∠QPN=90°,半径为PN=PM=PA=2.
∴劣弧NQ与两条半径所围成的扇形的面积=
=π.
