题目内容
(2006•西岗区)已知抛物线y= x2+bx+c经过点(1,-1)和C(0,-1),且与x轴交于A、B两点(A在B左边),直
x2+bx+c经过点(1,-1)和C(0,-1),且与x轴交于A、B两点(A在B左边),直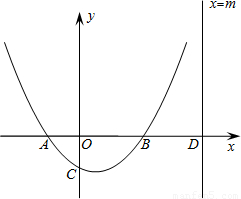 线x=m(m>0)与x轴交于点D.
线x=m(m>0)与x轴交于点D.(1)求抛物线的解析式;
(2)在第一象限内,直线x上是否存在点P,使得以P、B、D为顶点的三角形与△OBC全等?若存在,求出点P坐标;若不存在,说明理由;
(3)在(2)的情况下,过点P作x轴的平行线交抛物线于点Q,四边形AOPQ能否为平行四边形?若能,求Q点坐标;若不能,说明理由.
【答案】分析:(1)用待定系数法即可求出函数的解析式.
(2)本题要分两种情况进行讨论,由(1)不难得出A、B的坐标为(-1,0),(2,0).那么如果要使以P、B、D为顶点的三角形与△OBC全等,△PBD也必为直角三角形且以PB为斜边.
①当△PBD≌△BCO时,BD=OC=1,PD=OB=2,据此可求出P点的坐标.
②当△PBD≌△CBO时,BO=BD=2,PD=OC=1,据此可求出P点的坐标.
(3)如果四边形AOPQ为平行四边形,那么PQ平行且相等于OA,因此P点的坐标向坐标平移1个单位就是Q点的坐标,然后将其代入抛物线的解析式中,即可判断出Q点是否在抛物线上.
解答:解:(1)依题意,有:
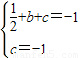 ,
,
解得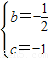
∴抛物线的解析式为y= x2-
x2- x-1.
x-1.
(2)易知:A(-1,0),B(2,0),C(0,-1);
∴OB=2,OC=1
①△PBD≌△BCO,BD=OC=1,PD=OB=2
∴OD=3,即P点坐标为(3,2).
②△PBD≌△CBO,BO=BD=2,PD=OC=1,
∴OD=4,即P点坐标为(4,1).
(3)∵四边形AOPQ为平行四边形,
∴PQ∥=OA
①当P点坐标为(3,2)时,Q点坐标为(2,2).
当x=2时,y= ×22-
×22- ×2-1=0,
×2-1=0,
因此这个Q点不在抛物线上.
②当P点坐标为(4,1)时,Q点坐标为(3,1).
当x=3时,y= ×32-
×32- ×3-1=2
×3-1=2
因此Q点不在抛物线上.
综上所述,不存在符合条件的Q点.
点评:本题着重考查了待定系数法求二次函数解析式、三角形全等、平行四边形的判定和性质等重要知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.
(2)本题要分两种情况进行讨论,由(1)不难得出A、B的坐标为(-1,0),(2,0).那么如果要使以P、B、D为顶点的三角形与△OBC全等,△PBD也必为直角三角形且以PB为斜边.
①当△PBD≌△BCO时,BD=OC=1,PD=OB=2,据此可求出P点的坐标.
②当△PBD≌△CBO时,BO=BD=2,PD=OC=1,据此可求出P点的坐标.
(3)如果四边形AOPQ为平行四边形,那么PQ平行且相等于OA,因此P点的坐标向坐标平移1个单位就是Q点的坐标,然后将其代入抛物线的解析式中,即可判断出Q点是否在抛物线上.
解答:解:(1)依题意,有:
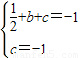 ,
,解得
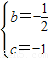
∴抛物线的解析式为y=
 x2-
x2- x-1.
x-1.(2)易知:A(-1,0),B(2,0),C(0,-1);
∴OB=2,OC=1
①△PBD≌△BCO,BD=OC=1,PD=OB=2
∴OD=3,即P点坐标为(3,2).
②△PBD≌△CBO,BO=BD=2,PD=OC=1,
∴OD=4,即P点坐标为(4,1).
(3)∵四边形AOPQ为平行四边形,
∴PQ∥=OA
①当P点坐标为(3,2)时,Q点坐标为(2,2).
当x=2时,y=
 ×22-
×22- ×2-1=0,
×2-1=0,因此这个Q点不在抛物线上.
②当P点坐标为(4,1)时,Q点坐标为(3,1).
当x=3时,y=
 ×32-
×32- ×3-1=2
×3-1=2因此Q点不在抛物线上.
综上所述,不存在符合条件的Q点.
点评:本题着重考查了待定系数法求二次函数解析式、三角形全等、平行四边形的判定和性质等重要知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
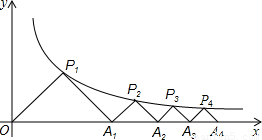
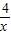 (x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.
(x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.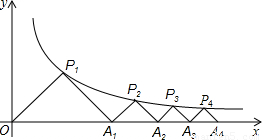
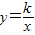 的图象过点A(-2,
的图象过点A(-2, ),则k的值为 .
),则k的值为 .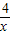 (x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.
(x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.