题目内容
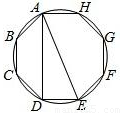
 如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则这个正八边形的面积为
如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则这个正八边形的面积为40
40
.分析:过C作CL⊥AD于L,连接HE,设正八边形的边长为a,AD=h;先根据△ADE的面积求出矩形ADEH的面积,再根据正多边形内角和定理求出各内角的度数,判断出△CDL的形状,求出边长;进一步可求出梯形ABCD的面积,根据S正八边形ABCDEFGH=S梯形ABCD+S梯形ABCD+S矩形ADEH即可解答.
解答: 解:取AE中点I,则点I为圆的圆心,圆内接正八边形ABCDEFGH是由8个与△IDE全等的三角形构成.易得△IDE的面积为5,则圆内接正八边形ABCDEFGH为8×5=40.
解:取AE中点I,则点I为圆的圆心,圆内接正八边形ABCDEFGH是由8个与△IDE全等的三角形构成.易得△IDE的面积为5,则圆内接正八边形ABCDEFGH为8×5=40.
故答案为40.
 解:取AE中点I,则点I为圆的圆心,圆内接正八边形ABCDEFGH是由8个与△IDE全等的三角形构成.易得△IDE的面积为5,则圆内接正八边形ABCDEFGH为8×5=40.
解:取AE中点I,则点I为圆的圆心,圆内接正八边形ABCDEFGH是由8个与△IDE全等的三角形构成.易得△IDE的面积为5,则圆内接正八边形ABCDEFGH为8×5=40.故答案为40.
点评:本题比较复杂,涉及到正多边形的性质、直角三角形的性质及梯形的面积公式,解答此题的关键是作出辅助线构造出直角三角形解答.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
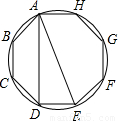
 如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为何( )
如图,有一圆内接正八边形ABCDEFGH,若△ADE的面积为10,则正八边形ABCDEFGH的面积为何( )| A、40 | B、50 | C、60 | D、80 |