题目内容
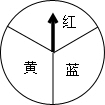 如图是一个可以自由转动的转盘,转盘被分成面积相等的3个扇形,转动转盘后任其自由停止,其中某个扇形会恰好停在指针所指的位置(如果指针恰好停在分割线上,那么重转一次)
如图是一个可以自由转动的转盘,转盘被分成面积相等的3个扇形,转动转盘后任其自由停止,其中某个扇形会恰好停在指针所指的位置(如果指针恰好停在分割线上,那么重转一次)
(1)转盘转动一次,指针所指的颜色不是红色的概率是多少?
(2)转盘转动两次,两次指针指向颜色相同的概率是多少?(用列表法或画树状图).
解:(1)转盘转动一次,指针所指的颜色不是红色的概率= ;
;
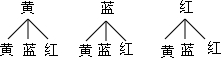
(2)画树状图如下:
 ,
,
共有9种等可能的结果,其中颜色相同占3种,
所以转盘转动两次,两次指针指向颜色相同的概率=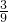 =
= .
.
分析:(1)由于颜色为蓝色或黄色转盘面积的三分之二,所以根据概率的定义得到指针所指的颜色不是红色的概率= ;
;
(2)先化树状图展示所有9种等可能的结果,其中颜色相同占3种,然后根据概率定义求解.
点评:本题考查了列表法与树状图法:先通过列表法或树状图法展示一个实验发生的所有等可能的结果,再从中找出某事件发生的结果数,然后根据概率的定义求这个事件的概率.
 ;
;(2)画树状图如下:
 ,
,共有9种等可能的结果,其中颜色相同占3种,
所以转盘转动两次,两次指针指向颜色相同的概率=
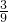 =
= .
.分析:(1)由于颜色为蓝色或黄色转盘面积的三分之二,所以根据概率的定义得到指针所指的颜色不是红色的概率=
 ;
;(2)先化树状图展示所有9种等可能的结果,其中颜色相同占3种,然后根据概率定义求解.
点评:本题考查了列表法与树状图法:先通过列表法或树状图法展示一个实验发生的所有等可能的结果,再从中找出某事件发生的结果数,然后根据概率的定义求这个事件的概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是一个可以自由转动的转盘,转动转盘转出数字“8”的可能性是( )
如图是一个可以自由转动的转盘,转动转盘转出数字“8”的可能性是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 4、如图是一个可以自由转动的转盘,转动这个转盘后,转出可能性最小的颜色是( )
4、如图是一个可以自由转动的转盘,转动这个转盘后,转出可能性最小的颜色是( )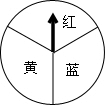 如图是一个可以自由转动的转盘,转盘被分成面积相等的3个扇形,转动转盘后任其自由停止,其中某个扇形会恰好停在指针所指的位置(如果指针恰好停在分割线上,那么重转一次)
如图是一个可以自由转动的转盘,转盘被分成面积相等的3个扇形,转动转盘后任其自由停止,其中某个扇形会恰好停在指针所指的位置(如果指针恰好停在分割线上,那么重转一次) 如图是一个可以自由转动的转盘,转盘被分成四个扇形,并分别标上1,2,3,4这四个数字.如果转动转盘一次(指针落在等分线上重转),转盘停止后,则指针指向的数字为偶数的概率是( )
如图是一个可以自由转动的转盘,转盘被分成四个扇形,并分别标上1,2,3,4这四个数字.如果转动转盘一次(指针落在等分线上重转),转盘停止后,则指针指向的数字为偶数的概率是( )