题目内容
在同一直角坐标系中反比例函数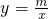 的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(-2,3),若一次函数的图象又与x轴相交于点B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(-2,3),若一次函数的图象又与x轴相交于点B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
解:将点A(-2,3)代入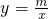 中得,m=-2×3=-6,
中得,m=-2×3=-6,
∴m=-6
∴y=-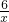 ,
,
又∵△AOB的面积为6,
∴ •OB•3=6,
•OB•3=6,
∴OB=4,
∴B点坐标为(4,0)或(-4,0),
①当B(4,0)时,
∵点A(-2,3)是两函数的交点,
∴ ,
,
解得k=- ,b=2,
,b=2,
∴y=- x+2;
x+2;
②当B(-4,0)时,
∵点A(-2,3)是两函数的交点,
∴ ,
,
解得k= ,b=6,
,b=6,
∴y= x+6.
x+6.
所以一次函数的解析式为y=- x+2或y=
x+2或y= x+6;反比例函数的解析式为y=-
x+6;反比例函数的解析式为y=-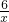 .
.
分析:将点A(-2,3)代入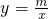 中得,得到m=-2×3=-6,即得到反比例函数的解析式;由△AOB的面积为6,求出OB,得到B点坐标为(4,0)或(-4,0),然后分类讨论:
中得,得到m=-2×3=-6,即得到反比例函数的解析式;由△AOB的面积为6,求出OB,得到B点坐标为(4,0)或(-4,0),然后分类讨论:
一次函数y=kx+b过(-2,3)和(4,0)或一次函数y=kx+b过(-2,3)和(-4,0),利用待定系数法求出一次函数的解析式.
点评:本题考查了利用待定系数法求函数的解析式;也考查了分类讨论思想的运用以及三角形的面积公式.
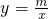 中得,m=-2×3=-6,
中得,m=-2×3=-6,∴m=-6
∴y=-
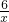 ,
,又∵△AOB的面积为6,
∴
 •OB•3=6,
•OB•3=6,∴OB=4,
∴B点坐标为(4,0)或(-4,0),
①当B(4,0)时,
∵点A(-2,3)是两函数的交点,
∴
 ,
,解得k=-
 ,b=2,
,b=2,∴y=-
 x+2;
x+2;②当B(-4,0)时,
∵点A(-2,3)是两函数的交点,
∴
 ,
,解得k=
 ,b=6,
,b=6,∴y=
 x+6.
x+6.所以一次函数的解析式为y=-
 x+2或y=
x+2或y= x+6;反比例函数的解析式为y=-
x+6;反比例函数的解析式为y=-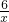 .
.分析:将点A(-2,3)代入
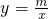 中得,得到m=-2×3=-6,即得到反比例函数的解析式;由△AOB的面积为6,求出OB,得到B点坐标为(4,0)或(-4,0),然后分类讨论:
中得,得到m=-2×3=-6,即得到反比例函数的解析式;由△AOB的面积为6,求出OB,得到B点坐标为(4,0)或(-4,0),然后分类讨论:一次函数y=kx+b过(-2,3)和(4,0)或一次函数y=kx+b过(-2,3)和(-4,0),利用待定系数法求出一次函数的解析式.
点评:本题考查了利用待定系数法求函数的解析式;也考查了分类讨论思想的运用以及三角形的面积公式.

练习册系列答案
相关题目
 直角坐标系中反比例函数
直角坐标系中反比例函数 的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(﹣2,3),若一次函数的图象又与x轴相交于点
的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(﹣2,3),若一次函数的图象又与x轴相交于点 B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式. 的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(-2,3),若一次函数的图象又与x轴相交于点B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(-2,3),若一次函数的图象又与x轴相交于点B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式. 的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(-2,3),若一次函数的图象又与x轴相交于点B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(-2,3),若一次函数的图象又与x轴相交于点B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.