题目内容
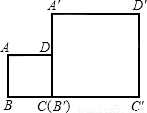
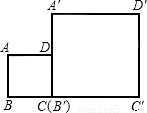
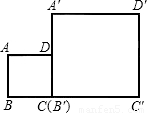
如图，现有两个边长为1：2的正方形ABCD与A′B′C′D′，已知B，C，B′，C′在同一直线上，且点C与点B′重合，请你利用这两个正方形，通过截割，平移，旋转的方法，拼出两个相似比为1：3的三角形．要求：（1）借助原图拼图；
（2）简要说明方法；
（3）指明相似的两个三角形．
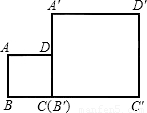
【答案】分析：由题意可知，A'D'：BC'=2：3，所以可平分A'D'，通过连接BD并延长交A′D′于点E，交C′D′延长线于点F，即可平分，且所得△ADB≌△A'ED≌△DEF，将△DA′E绕点E旋转至△FD′E的位置，则△BAD∽△FC′B，且相似比为1：3．
解答：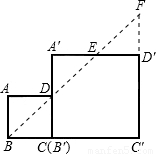
解：
方法：①连接BD并延长交A′D′于点E，交C′D′延长线于点F；
②将△DA′E绕点E旋转至△FD′E的位置，则△BAD∽△FC′B，且相似比为1：3．
点评：此题主要利用了相似三角形的判定和正方形、旋转的性质等作图，难度中等．
解答：
解：方法：①连接BD并延长交A′D′于点E，交C′D′延长线于点F；
②将△DA′E绕点E旋转至△FD′E的位置，则△BAD∽△FC′B，且相似比为1：3．
点评：此题主要利用了相似三角形的判定和正方形、旋转的性质等作图，难度中等．
练习册系列答案
阅读快车系列答案
相关题目
（2004•烟台）如图，现有两个边长为1：2的正方形ABCD与A′B′C′D′，已知B，C，B′，C′在同一直线上，且点C与点B′重合，请你利用这两个正方形，通过截割，平移，旋转的方法，拼出两个相似比为1：3的三角形．
