题目内容
如图,已知直线y=-
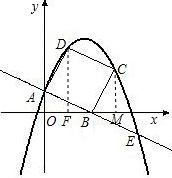
x+1交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过 点A,D,C的抛物线与直线的另一个交点为E.
点A,D,C的抛物线与直线的另一个交点为E.
(1)直接写出点C和点D的坐标,C(______)、D(______);
(2)求出过A,D,C三点的抛物线的解析式.
| 1 |
| 2 |
 点A,D,C的抛物线与直线的另一个交点为E.
点A,D,C的抛物线与直线的另一个交点为E.(1)直接写出点C和点D的坐标,C(______)、D(______);
(2)求出过A,D,C三点的抛物线的解析式.
(1)直线y=-
x+1中,
令y=0,得x=2,令x=0,得y=1;
∴A(0,1),B(2,0);
过C作CM⊥x轴于M;
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°;
∵∠AOB=90°,
∴∠ABO+∠BAO=∠ABO+∠CBM=90°,
即∠BAO=∠CBM;
∴Rt△ABO≌Rt△BCM;
∴BM=OA=1,CM=OB=2,即OM=OB+BM=3;
∴C(3,2),
过D点作DF⊥x轴于点F,可知OF=1,DF=3,
∴D(1,3);
∴C、D的坐标分别为:C(3,2),D(1,3)(每空2分)
(2)把x=0代入y=-
x+1得,y=1
∴A点坐标为(0,1)(1分)
设二次函数的解析式为y=ax2+bx+c(a≠0).
把点A(0,1),C(3,2),D(1,3)代入得
(2分)
解得
∴二次函数的解析式为y=-
x2+
x+1.(2分)
| 1 |
| 2 |
令y=0,得x=2,令x=0,得y=1;
∴A(0,1),B(2,0);
过C作CM⊥x轴于M;
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°;
∵∠AOB=90°,
∴∠ABO+∠BAO=∠ABO+∠CBM=90°,
即∠BAO=∠CBM;
∴Rt△ABO≌Rt△BCM;
∴BM=OA=1,CM=OB=2,即OM=OB+BM=3;
∴C(3,2),
过D点作DF⊥x轴于点F,可知OF=1,DF=3,
∴D(1,3);
∴C、D的坐标分别为:C(3,2),D(1,3)(每空2分)
(2)把x=0代入y=-
| 1 |
| 2 |
∴A点坐标为(0,1)(1分)
设二次函数的解析式为y=ax2+bx+c(a≠0).
把点A(0,1),C(3,2),D(1,3)代入得
|
解得
|
∴二次函数的解析式为y=-
| 5 |
| 6 |
| 17 |
| 6 |


练习册系列答案
相关题目
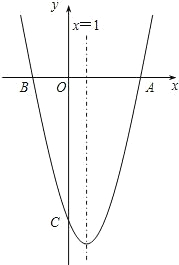 段OC的长度是线段OA的2倍,抛物线的对称轴是直线x=1.
段OC的长度是线段OA的2倍,抛物线的对称轴是直线x=1.
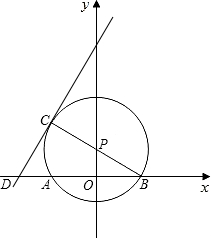 的直线y=2x+b交x轴于D,且⊙P的半径为
的直线y=2x+b交x轴于D,且⊙P的半径为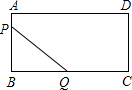 就停止移动.据此解答下列问题:
就停止移动.据此解答下列问题: