题目内容
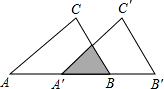 如图,把△ABC沿着AB的方向平移到△A′B′C′的位置,使它们重叠部分的面积(图中阴影)是△ABC面积的四分之一,若AB=2,则此三角形移动的距离AA′是
如图,把△ABC沿着AB的方向平移到△A′B′C′的位置,使它们重叠部分的面积(图中阴影)是△ABC面积的四分之一,若AB=2,则此三角形移动的距离AA′是
- A.

- B.

- C.

- D.1
D
分析:根据平移得出AC∥A′C′,推出△A′OB∽△ACB,根据相似三角形的面积之比等于相似比的平方得出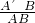 =
= ,代入求出即可.
,代入求出即可.
解答:∵把△ABC沿着AB的方向平移到△A′B′C′的位置,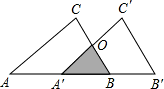
∴AC∥A′C′,
∴△A′OB∽△ACB,
∵重叠部分的面积A′OB是△ABC面积的四分之一,
∴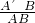 =
= ,
,
∵AB=2,
∴A′B=1.
故选D.
点评:本题考查了平移的性质和相似三角形的性质和判定,注意:相似三角形的面积之比等于相似比的平方.
分析:根据平移得出AC∥A′C′,推出△A′OB∽△ACB,根据相似三角形的面积之比等于相似比的平方得出
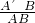 =
= ,代入求出即可.
,代入求出即可.解答:∵把△ABC沿着AB的方向平移到△A′B′C′的位置,

∴AC∥A′C′,
∴△A′OB∽△ACB,
∵重叠部分的面积A′OB是△ABC面积的四分之一,
∴
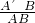 =
= ,
,∵AB=2,
∴A′B=1.
故选D.
点评:本题考查了平移的性质和相似三角形的性质和判定,注意:相似三角形的面积之比等于相似比的平方.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
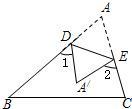 3、如图,把△ABC纸片沿着DE折叠,当点A落在四边形BCED内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
3、如图,把△ABC纸片沿着DE折叠,当点A落在四边形BCED内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
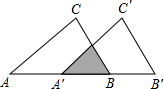 如图,把△ABC沿着AB的方向平移到△A′B′C′的位置,使它们重叠部分的面积(图中阴影)是△ABC面积的四分之一,若AB=2,则此三角形移动的距离AA′是( )
如图,把△ABC沿着AB的方向平移到△A′B′C′的位置,使它们重叠部分的面积(图中阴影)是△ABC面积的四分之一,若AB=2,则此三角形移动的距离AA′是( )