题目内容
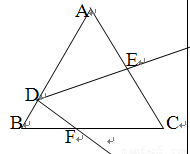
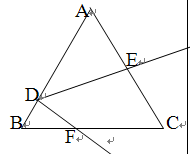
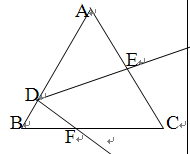
已知如图:等边△ABC中,D是AB上一点,∠EDF=60o,则tan∠AED=

- A.tan∠B
- B.tan∠BFD
- C.tan∠ADE
- D.tan∠BDF
D
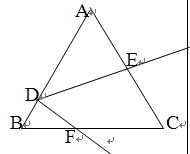
如图
因为三角形ABC为等边三角形,所以∠A=60 o
又∠A+∠AED+∠ADE=180 o 即60o+∠AED+∠ADE=180 o
又∠EDF+∠BDF+∠ADE=180 o
因为∠EDF=60o 上式即60o+∠BDF+∠ADE=180 o
所以∠AED=∠BDF
故选D

如图
因为三角形ABC为等边三角形,所以∠A=60 o
又∠A+∠AED+∠ADE=180 o 即60o+∠AED+∠ADE=180 o
又∠EDF+∠BDF+∠ADE=180 o
因为∠EDF=60o 上式即60o+∠BDF+∠ADE=180 o
所以∠AED=∠BDF
故选D

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知如图:等边△ABC中,D是AB上一点,∠EDF=60o,则tan∠AED=( )。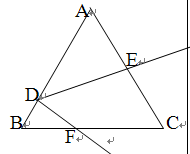
| A.tan∠B | B.tan∠BFD | C.tan∠ADE | D.tan∠BDF |
已知如图:等边△ABC中,D是AB上一点,∠EDF=60o,则tan∠AED=( )。

| A.tan∠B | B.tan∠BFD | C.tan∠ADE | D.tan∠BDF |