题目内容
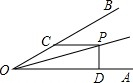 已知:如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=6,则PD=
已知:如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=6,则PD=3
3
.分析:过P作PE⊥OB于E,根据角平分线性质求出PE=PD,根据平行线性质得出∠ECP=30°,根据含30度角性质求出PE即可.
解答: 解:过P作PE⊥OB于E,
解:过P作PE⊥OB于E,
∵∠AOP=∠BOP,PD⊥OA,
∴PE=PD,
∵PC∥OA,
∴∠CPO=∠POA=15°=∠BOP,
∴∠ECP=∠BOP+∠CPO=30°,
∵∠PEC=90°,
∴PE=
PC=
×6=3,
即PD=PE=3.
故答案为:3.
 解:过P作PE⊥OB于E,
解:过P作PE⊥OB于E,∵∠AOP=∠BOP,PD⊥OA,
∴PE=PD,
∵PC∥OA,
∴∠CPO=∠POA=15°=∠BOP,
∴∠ECP=∠BOP+∠CPO=30°,
∵∠PEC=90°,
∴PE=
| 1 |
| 2 |
| 1 |
| 2 |
即PD=PE=3.
故答案为:3.
点评:本题考查了角平分线性质,平行线性质,含30度角的直角三角形等知识点,关键是正确作辅助线后求出PE=PD和求出PE长,题目比较典型,是一道比较好的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
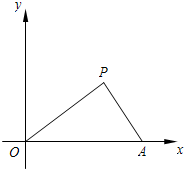 (2007•上海模拟)已知:如图,在△OAP中,OA=6,sin∠POA=
(2007•上海模拟)已知:如图,在△OAP中,OA=6,sin∠POA=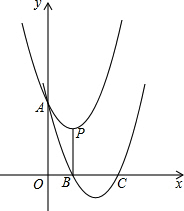 (2013•闸北区二模)已知:如图,抛物线y=x2-2x+3与y轴交于点A,顶点是点P,过点P作PB⊥x轴于点B.平移该抛物线,使其经过A、B两点.
(2013•闸北区二模)已知:如图,抛物线y=x2-2x+3与y轴交于点A,顶点是点P,过点P作PB⊥x轴于点B.平移该抛物线,使其经过A、B两点.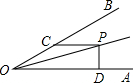 已知:如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=6,则PD=________.
已知:如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA于D,若PC=6,则PD=________.