题目内容
【题目】在△ABC中,CE,BD分别是边AB,AC上的高,F是BC边上的中点.
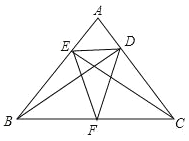
(1)指出图中的一个等腰三角形,并说明理由.
(2)若∠A=x°,求∠EFD的度数(用含x的代数式表达).
(3)猜想∠ABC和∠EDA的数量关系,并证明.
【答案】(1)△DEF是等腰三角形;
(2)∠EFD=180°﹣2x°;
(3)ABC=∠EDA.
【解析】
试题分析:(1)根据直角三角形的性质得到EF=![]() BC,DF=
BC,DF=![]() BC,等量代换即可;
BC,等量代换即可;
(2)根据三角形内角和定理和等腰三角形的性质计算;
(3)根据圆内接四边形的性质解答.
试题解析:(1)△DEF是等腰三角形.
∵CE,BD分别是边AB,AC上的高,F是BC边上的中点,
∴EF=![]() BC,DF=
BC,DF=![]() BC,
BC,
∴EF=DF,
∴△DEF是等腰三角形;
(2)∵FE=FB,FD=FC,
∴∠FEB=∠FBE,∠FDC=∠FCD,
∴∠FEB+∠FDC=∠FBE+∠FCD=180°﹣∠A=180°﹣x°,
∠AED+∠ADE=180°﹣∠A=180°﹣x°,
∴∠FED+∠FDE=360°﹣(180°﹣x°)﹣(180°﹣x°)=2x°,
∴∠EFD=180°﹣2x°;
(3)∠ABC=∠EDA.
∵∠BEC=∠BDC=90°,
∴B、E、D、C四点共圆,
∴∠ABC=∠EDA.

练习册系列答案
相关题目