Question

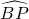如图1所示为三角形纸片ABC，上有一点P．已知将A，B，C往内折至P时，出现折线，，，其中Q、R、S、T四点会分别在，，，上，如图2所示．若△ABC、四边形PTQR的面积分别为16、5，则△PRS面积为

1. A.
   1
2. B.
   2
3. C.
   3
4. D.
   4

Answer 1

C
分析：根据折叠，知△BTQ的面积和△PTQ的面积相等，△CQR和△PQR的面积相等，△ASR的面积和△PSR的面积相等，结合已知△ABC、四边形PTQR的面积分别为16、5，即可求解．
解答：根据题意，得
△BTQ的面积和△PTQ的面积相等，△CQR和△PQR的面积相等，△ASR的面积和△PSR的面积相等．
又△ABC、四边形PTQR的面积分别为16、5，
∴△PRS面积等于（16-5×2）÷2=3．
故选C．
点评：此题主要是能够根据折叠，得到重合图形的面积相等．