题目内容
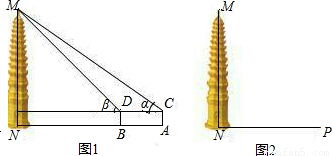
(2009•济宁)坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋(公元1112年),为砖彻八角形十三层楼阁式建筑.数学活动小组开展课外实践活动,在一个阳光明媚的上午,他们去测量太子灵踪塔的高度,携带的测量工具有:测角仪、皮尺、小镜子.(1)小华利用测角仪和皮尺测量塔高.图1为小华测量塔高的示意图.她先在塔前的平地上选择一点A,用测角仪测出看塔顶(M)的仰角α=35°,在A点和塔之间选择一点B,测出看塔顶(M)的仰角β=45°,然后用皮尺量出A、B两点的距离为18.6m,自身的高度为1.6m.请你利用上述数据帮助小华计算出塔的高度;(tan35°≈0.7,结果保留整数)
(2)如果你是活动小组的一员,正准备测量塔高,而此时塔影NP的长为am(如图2),你能否利用这一数据设计一个测量方案如果能,请回答下列问题:
①在你设计的测量方案中,选用的测量工具是:______;
②要计算出塔的高,你还需要测量哪些数据______.

【答案】分析:(1)设CD的延长线交MN于E点,MN长为x,根据题意构造直角三角形,利用其公共边构造方程求解.
(2)根据题目中的情景,结合解三角形的知识设计测量方法.
解答: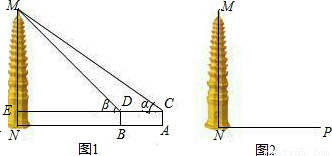 解:(1)设CD的延长线交MN于E点,MN长为x,
解:(1)设CD的延长线交MN于E点,MN长为x,
则ME=x-1.6.
∵β=45°,
∴tanβ=ME:EB=1,
∴BE=ME
∴DE=ME=x-1.6.
∴CE=x-1.6+18.6=x+17.
∵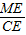 =tanα=tan35°,
=tanα=tan35°,
∴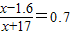 ,
,
解得x=45.
∴太子灵踪塔(MN)的高度为45m.
(2)①测角仪、皮尺;
②站在P点看塔顶的仰角、自身的高度.
点评:本题考查仰角的应用:要求学生借助仰角关系构造直角三角形,并结合图形解三角形或设计测量方法.
(2)根据题目中的情景,结合解三角形的知识设计测量方法.
解答:
 解:(1)设CD的延长线交MN于E点,MN长为x,
解:(1)设CD的延长线交MN于E点,MN长为x,则ME=x-1.6.
∵β=45°,
∴tanβ=ME:EB=1,
∴BE=ME
∴DE=ME=x-1.6.
∴CE=x-1.6+18.6=x+17.
∵
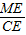 =tanα=tan35°,
=tanα=tan35°,∴
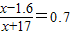 ,
,解得x=45.
∴太子灵踪塔(MN)的高度为45m.
(2)①测角仪、皮尺;
②站在P点看塔顶的仰角、自身的高度.
点评:本题考查仰角的应用:要求学生借助仰角关系构造直角三角形,并结合图形解三角形或设计测量方法.

练习册系列答案
相关题目