题目内容
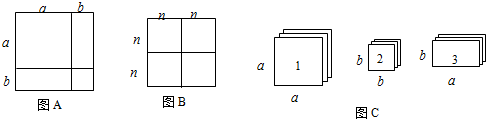
 我们知道,代数恒等式都可以用面积的方法来加以验证它的正确性,用图形的拼接我们可以发现更多的代数恒等式,图是由4个长为m、宽为n的小长方形拼成的大长方形.
我们知道,代数恒等式都可以用面积的方法来加以验证它的正确性,用图形的拼接我们可以发现更多的代数恒等式,图是由4个长为m、宽为n的小长方形拼成的大长方形.(1)写出图中所表示的代数恒等式
2m×2n=4mn
2m×2n=4mn
;(2)请再用这4个小长方形,画一个几何图形,使它验证的恒等式为:(m+n)2-(m-n)2=4mn;
(3)若x+y=-6,xy=2.75,则x-y=
±5
±5
.分析:(1)根据矩形面积求出即可;
(2)利用4个矩形面积得出(m+n)2-(m-n)2=4mn即可;
(3)根据(x+y)2=x2+y2+2xy=36,得出x2+y2+2×2.75=36,即可得出x2+y2=30.5,得出(x-y)2=25,即可得出答案.
(2)利用4个矩形面积得出(m+n)2-(m-n)2=4mn即可;
(3)根据(x+y)2=x2+y2+2xy=36,得出x2+y2+2×2.75=36,即可得出x2+y2=30.5,得出(x-y)2=25,即可得出答案.
解答:解:(1)根据矩形面积得出:2m×2n=4mn,
故答案为:2m×2n=4mn;
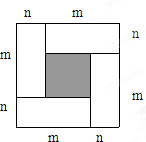
(2)如图所示:(m+n)2-(m-n)2=4mn,
 ;
;
(3)∵x+y=-6,xy=2.75,
∴(x+y)2=x2+y2+2xy=36,
∴x2+y2+2×2.75=36,
∴x2+y2=30.5,
则(x-y)2=x2+y2-2xy=30.5-5.5=25,
∴x-y=±5,
故答案为:±5.
故答案为:2m×2n=4mn;
(2)如图所示:(m+n)2-(m-n)2=4mn,
 ;
;(3)∵x+y=-6,xy=2.75,
∴(x+y)2=x2+y2+2xy=36,
∴x2+y2+2×2.75=36,
∴x2+y2=30.5,
则(x-y)2=x2+y2-2xy=30.5-5.5=25,
∴x-y=±5,
故答案为:±5.
点评:此题主要考查了完全平方公式的应用,根据矩形面积得出公式是解题关键.

练习册系列答案
相关题目
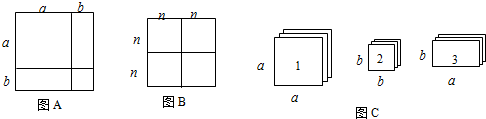
 ,实际上利用一些卡片拼成的图形面积也可以
,实际上利用一些卡片拼成的图形面积也可以
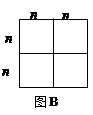

 的矩形,则需要1号卡片 张,2号卡片 张,
的矩形,则需要1号卡片 张,2号卡片 张,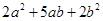 ,并利用你画的图形面积对
,并利用你画的图形面积对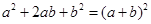 ,实际上利用一些卡片拼成的图形面积也可以
,实际上利用一些卡片拼成的图形面积也可以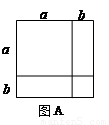
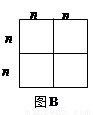

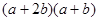 的矩形,则需要1号卡片 张,2号卡片 张,
的矩形,则需要1号卡片 张,2号卡片 张,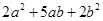 ,并利用你画的图形面积对
,并利用你画的图形面积对