题目内容
如图,直线l1与坐标轴分别交于点A、B,经过原点的直线l2与AB交于点C,与过点A且平行于y轴的直线交于点D,已知点C(3,| 15 |
| 4 |
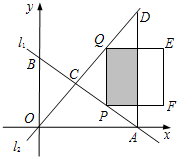 的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.
的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.(1)点求直线l1的解析式;
(2)当点P在线段AC上时,试求正方形PQEF与△ACD重叠部分(阴影部分)的面积的最大值;
(3)设点M坐标为(4,
| 9 |
| 2 |
分析:(1)本题需先根据已知条件,设出直线l1的解析式再根据C点的坐标和OA的长,求出k与b的值来,即可求出结果.
(2)先根据题意得出P、Q点的坐标,从而解出t的值,然后再分两种情况进行讨论,分别得出S的最大值,及可求出结果.
(3)本题分两种情况进行讨论,当t<3时和t>3时,分别求出t的取值范围,即可求出结果.
(2)先根据题意得出P、Q点的坐标,从而解出t的值,然后再分两种情况进行讨论,分别得出S的最大值,及可求出结果.
(3)本题分两种情况进行讨论,当t<3时和t>3时,分别求出t的取值范围,即可求出结果.
解答:解:(1)设直线l1的解析式为y=kx+b,
∵直线l1与直线l2交于点C,
又∵OA=8,
∴把C(3,
),A(8,0)代入上式得:
,
解得:b=6,k=-
,
∴直线l1的解析式为:y=-
x+6;
(2)点P在线段AC上时,根据题意有:P(t,-
t+6),Q(t,
t),
∴PQ=
t-(-
t+6)=2t-6,
当EF在AD上时,t+2t-6=8,有t=
,
当3<t≤
时,S=(2t-6)2,
当t=
时,S最大=
,
当
≤t≤8时,S=(2t-6)(8-t)=-2(t-
)2+
,
当t=
时,S最大=
;
所以,S的最大值为
;
(3)当t<3时,有
,
解得:t<2,
当t>3时,有
,
解得:3.6<t<4,
点M能在正方形PQEF内部,此时t的取值范围是3.6<t<4或t<2.
∵直线l1与直线l2交于点C,
又∵OA=8,
∴把C(3,
| 15 |
| 4 |
|
解得:b=6,k=-
| 3 |
| 4 |
∴直线l1的解析式为:y=-
| 3 |
| 4 |
(2)点P在线段AC上时,根据题意有:P(t,-
| 3 |
| 4 |
| 5 |
| 4 |
∴PQ=
| 5 |
| 4 |
| 3 |
| 4 |
当EF在AD上时,t+2t-6=8,有t=
| 14 |
| 3 |
当3<t≤
| 14 |
| 3 |
当t=
| 14 |
| 3 |
| 100 |
| 9 |
当
| 14 |
| 3 |
| 11 |
| 2 |
| 25 |
| 2 |
当t=
| 11 |
| 2 |
| 25 |
| 2 |
所以,S的最大值为
| 25 |
| 2 |
(3)当t<3时,有
|
解得:t<2,
当t>3时,有
|
解得:3.6<t<4,
点M能在正方形PQEF内部,此时t的取值范围是3.6<t<4或t<2.
点评:本题主要考查了一次函数的综合应用,解题时要注意知识的综合运用,是一道很好的题.

练习册系列答案
相关题目
 (2011•裕华区二模)如图,直线l1与l2相交于点P,点P横坐标为-1,l1的解析表达式为y=
(2011•裕华区二模)如图,直线l1与l2相交于点P,点P横坐标为-1,l1的解析表达式为y= 已知:如图,直线l1与y轴交点坐标为(0,-1),直线l2与x轴交点坐标为(3,0),两直线交点为P(1,1),解答下面问题:
已知:如图,直线l1与y轴交点坐标为(0,-1),直线l2与x轴交点坐标为(3,0),两直线交点为P(1,1),解答下面问题: 如图,直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).
如图,直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1). ),且OA=8.在直线AB上取点P,过点P作y轴
),且OA=8.在直线AB上取点P,过点P作y轴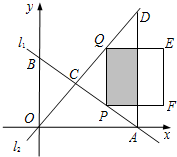 的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.
的平行线,与CD交于点Q,以PQ为边向右作正方形PQEF.设点P的横坐标为t.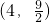 ,在点P的运动过程中,点M能否在正方形PQEF内部?若能,求出t的取值范围;若不能,试说明理由.
,在点P的运动过程中,点M能否在正方形PQEF内部?若能,求出t的取值范围;若不能,试说明理由.