题目内容
【题目】在△ABC中，∠C=90°，AC=BC．作射线AP，过点B作BD⊥AP于点D，连接CD．
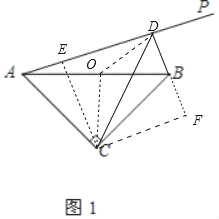
（1）当射线AP位于图1所示的位置时
①根据题意补全图形；
②求证：AD+BD=
CD．
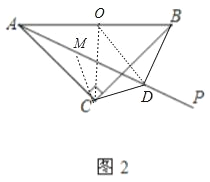
（2）当射线AP绕点A由图1的位置顺时针旋转至∠BAC的内部，如图2，直接写出此时AD，BD，CD三条线段之间的数量关系为 ．
【答案】（1）①见解析；②见解析；（2）结论：AD﹣BD= CD．理由见解析．
【解析】
（1）①根据要求补全图形即可；
②取AB是中点O，连接OD、OC，作CE⊥AD于E，CF⊥DB于F．四只要证明边形DECF是正方形，可得DE=DF，CD= 
DE
由Rt△CAE≌Rt△CBF，推出AE=BF，可得AB+DB=DE+AE+DF-BF=2DE，
（2）结论：AD-BD= CD,取AB的中点O，连接OC，OD．作CM⊥CD交AD于M．只要证明△MCD是等腰直角三角形，△ACM≌△BCD，、即可解决问题；
（1）解：①补全图的图形如图所示；
②证明：取AB是中点O，连接OD、OC，作CE⊥AD于E，CF⊥DB于F．
∵∠ACB=∠ADB=90°，
∴OC=OD=
AB，
∴A、D、B、C四点共圆，
∴∠ADB=∠ABC=45°，
∴∠ADC=∠CDB，
∵CE⊥AD于E，CF⊥DB于F，
∴CE=CF，
易证四边形DECF是正方形，
∴DE=DF，CD=DE，
∵AC=BC，CE=CF，
∴Rt△CAE≌Rt△CBF，
∴AE=BF，
∵AB+DB=DE+AE+DF﹣BF=2DE，
又∵DE=
CD，
∴AB+BD=CD．
（2）结论：AD﹣BD=CD．
理由：取AB的中点O，连接OC，OD．作CM⊥CD交AD于M．
∵∠ACB=∠ADB=90°，OA=OB，
∴OC=OD=AB，
∴A、C、D、B四点共圆，（设AD交BC于O，先证明△AOC∽△BOD，再证明△AOB∽△COD即可）
∴∠ADC=∠ABC=45°，
∴△MCD是等腰直角三角形，
∴CM=CD，
∵∠MCD=∠ACB=90°，
∴∠ACM=∠BCD，∵CA=CB，
∴△ACM≌△BCD，
∴AM=BD，
∴AD﹣BD=AD=AM=DM=CD．
故答案为：AD﹣BD=CD．
