题目内容
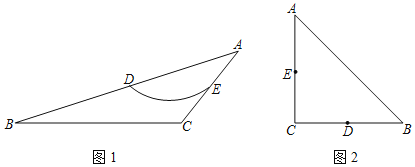
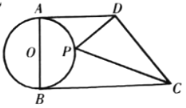
【题目】如图三角形ABC是圆O的内接正三角形,弦EF经过BC边的中点D,且EF平行AB,若AB等于6,则EF等于________.

【答案】![]()
【解析】
设AC与EF交于点G,由于EF∥AB,且D是BC中点,易得DG是△ABC的中位线,即DG=3;易知△CDG是等腰三角形,可过C作AB的垂线,交EF于M,交AB于N;然后证DE=FG,根据相交弦定理得BDDC=DEDF,而BD、DC的长易知,DF=3+DE,由此可得到关于DE的方程,即可求得DE的长,EF=DF+DE=3+2DE,即可求得EF的长;
解:如图,过C作CN⊥AB于N,交EF于M,则CM⊥EF,

根据圆和等边三角形的性质知:CN必过点O,
∵EF∥AB,D是BC的中点,
∴DG是△ABC的中位线,
即DG=![]() AB=3;
AB=3;
∵∠ACB=60°,BD=DC=![]() BC,AG=GC=
BC,AG=GC=![]() AC,且BC=AC,
AC,且BC=AC,
∴△CGD是等边三角形,
∵CM⊥DG,
∴DM=MG;
∵OM⊥EF,
由垂径定理得:EM=MF,
故DE=GF,
∵弦BC、EF相交于点D,
∴BD×DC=DE×DF,
即DE×(DE+3)=3×3;
解得DE=![]() 或
或![]() (舍去);
(舍去);
∴EF=3+2×![]() =
=![]() ;
;

练习册系列答案
相关题目