题目内容
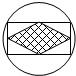
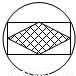
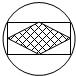 15、如图是一个徽章,圆圈中间是一个矩形,矩形中间是一个菱形,菱形的边长是1cm,那么徽章的直径是
15、如图是一个徽章,圆圈中间是一个矩形,矩形中间是一个菱形,菱形的边长是1cm,那么徽章的直径是2cm
.分析:四边形ABCD为圆的内接矩形,四边形EFQH为菱形,并且各顶点为矩形各边的中点,连AC,∠ABC=90°,得到AC为直径,易得EF∥AC,且AC=2EF,即可求出AC的长.
解答:解:如图,
四边形ABCD为圆的内接矩形,四边形EFQH为菱形,并且各顶点为矩形各边的中点,
连AC,
∵∠ABC=90°,
∴AC为直径,
又∵E,F分别为AB,BC的中点,
∴EF∥AC,且AC=2EF,
而菱形的边长是1cm,即EF=1cm,
∴AC=2cm,
即徽章的直径为2cm.

四边形ABCD为圆的内接矩形,四边形EFQH为菱形,并且各顶点为矩形各边的中点,
连AC,
∵∠ABC=90°,
∴AC为直径,
又∵E,F分别为AB,BC的中点,
∴EF∥AC,且AC=2EF,
而菱形的边长是1cm,即EF=1cm,
∴AC=2cm,
即徽章的直径为2cm.
点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了圆周角的推论:直径所对的圆周角为90度以及矩形和菱形的性质.

练习册系列答案
相关题目
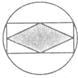 16、如图是一个俱乐部的徽章.徽章的图案是一个金色的圆圈,中间是一个矩形,矩形中间又有一个蓝色的菱形,徽章的直径为2cm,则徽章内的菱形的边长为
16、如图是一个俱乐部的徽章.徽章的图案是一个金色的圆圈,中间是一个矩形,矩形中间又有一个蓝色的菱形,徽章的直径为2cm,则徽章内的菱形的边长为 如图是一个徽章,圆圈中间是一个矩形,矩形中间是一个菱形,菱形的边长是1cm,那么徽章的直径是________.
如图是一个徽章,圆圈中间是一个矩形,矩形中间是一个菱形,菱形的边长是1cm,那么徽章的直径是________.