题目内容
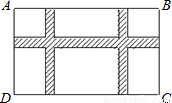
 14、如图,某小区规划在长32米,宽20米的矩形场地ABCD上修建三条同样宽的3条小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为570米2,问小路应为多宽?
14、如图,某小区规划在长32米,宽20米的矩形场地ABCD上修建三条同样宽的3条小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为570米2,问小路应为多宽?分析:设小路的宽为x米,能分别表示出三条小路的面积,从图上可以看出相加的时候重复加了2x2.可列方程求解.
解答:解:设小路宽为x米,则小路总面积为:20x+20x+32x-2•x2=32×20-570,
整理,得2x2-72x+70=0,
x2-36x+35=0,
∴(x-35)(x-1)=0,
∴x1=35(舍),x2=1,
∴小路宽应为1米.
整理,得2x2-72x+70=0,
x2-36x+35=0,
∴(x-35)(x-1)=0,
∴x1=35(舍),x2=1,
∴小路宽应为1米.
点评:解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题关键是把小路的宽设出来,然后看到重复的部分再去掉得到面积.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
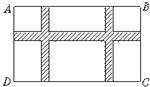
 25、如图,某小区规划在一个长40米,宽为26米的矩形场地ABCD上,修建三条同样宽的道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每块草坪的面积都为144平方米,求道路的宽度.
25、如图,某小区规划在一个长40米,宽为26米的矩形场地ABCD上,修建三条同样宽的道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每块草坪的面积都为144平方米,求道路的宽度. 如图,某小区规划在长32米,宽20米的矩形场地ABCD上修建三条同样宽的3条小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为570米2,问小路应为多宽?
如图,某小区规划在长32米,宽20米的矩形场地ABCD上修建三条同样宽的3条小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为570米2,问小路应为多宽?