题目内容
【题目】如图1,点P是线段AB上的动点(P不与A、B重合),分别以AP、BP为边向线段AB的同侧作等边△APC和等边△BPD,AD和BC交于点M. 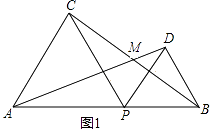
(1)求证:AD=BC;
(2)将点P在线段AB上随意固定,再把△BPD按顺时针方向绕点P旋转一个角度α(α<60°),如图2所示,在旋转过程中,∠AMC的度数是否与α的大小有关?证明你的结论. 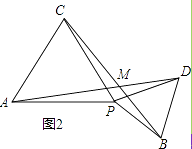
【答案】
(1)解:如图1,
∵△APC和△BPD是等边三角形,
∴CP=AP,DP=PB,∠APC=∠DPB=60°,
∵∠BPC=180°﹣60°,∠DPA=180°﹣60°,
∴∠BPC=∠DPA,
在△BPC和△DPA中,
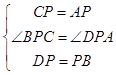 ,
,
∴△BPC≌△DPA,
∴AD=BC
(2)解:∠AMC的度数与α的大小无关,理由如下:
如图2,∵∠BPC=∠CPD+60°,∠DPA=∠CPD+60°,
∴∠BPC=∠DPA,
在△BPC和△DPA中,
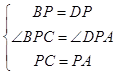 ,
,
∴△BPC≌△DPA,
∴∠BCP=∠DAP,
∴∠AMC=180°﹣∠MCP﹣∠PCA﹣∠MAC
=120°﹣∠BCP﹣∠MAC
=120°﹣(∠DAP+∠MAC)
=120°﹣∠PAC
=60°,
∴∠AMC的度数与α无关.
【解析】(1)只要证明△BPC≌△DPA即可.(2)先证明△BPC≌△DPA得到∠BCP=∠DAP,求出∠AMC的大小即可解决问题.
【考点精析】通过灵活运用等边三角形的性质,掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目