题目内容
如图，是由8个相同的小立方块搭成的几何体，它的三个视图都是2×2的正方形，若拿掉若干个小立方块后（几何体不倒掉），其三个视图仍都为2×2的正方形，则最多能拿掉小立方块的个数为（ ）
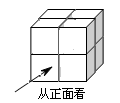
| A．1 | B．2 | C．3 | D．4 |
B
分析：拿掉若干个小立方块后保证几何体不倒掉，且三个视图仍都为2×2的正方形，所以最底下一层必须有四个小立方块，这样能保证俯视图仍为2×2的正方形，为保证正视图与左视图也为2×2的正方形，所以上面一层必须保留交错的两个立方块，即可知最多能拿掉小立方块的个数．
解答：解：根据题意，拿掉若干个小立方块后，三个视图仍都为2×2的正方形，
所以最多能拿掉小立方块的个数为2个．
故选B．
解答：解：根据题意，拿掉若干个小立方块后，三个视图仍都为2×2的正方形，
所以最多能拿掉小立方块的个数为2个．
故选B．
练习册系列答案
名校课堂系列答案
相关题目
，
。