题目内容
如图,以Rt△BCF的斜边BC为直径作⊙O,A为 |
| BF |
 |
| AB |
 |
| AF |
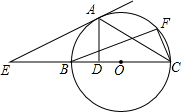 D,过A作AE∥BF交CB的延长线于E.
D,过A作AE∥BF交CB的延长线于E.求证:
(1)AE是⊙O切线;
(2)
| BD |
| CD |
| BE |
| EC |
(3)若⊙O直径为d,则
| 1 |
| CD |
| 1 |
| EC |
| 2 |
| d |
分析:(1)要证AE是⊙O切线,只要证明AE⊥OA即可;
(2)根据已知利用相似三角形的判定,再根据相似比之间的转化从而得到结论;
(3)根据相似三角形的边对应成比例即可证得结论.
(2)根据已知利用相似三角形的判定,再根据相似比之间的转化从而得到结论;
(3)根据相似三角形的边对应成比例即可证得结论.
解答: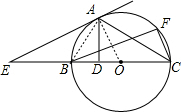 证明:(1)连接AB,OA,
证明:(1)连接AB,OA,
∵弧AB=弧AF,OA是⊙O的半径,
∴OA⊥BF.
∵AE∥EF,
∴AE⊥OA.
∵OA是⊙O的半径,
∴AE是⊙O切线.
(2)∵BC是⊙O的直径,
∴∠BAC=90°.
∵AD⊥BC,
∴△ABD∽△ABC,△ACD∽△ABC.
∴AB2=BD•BC,AC2=CD•BC,
∴
=
①
∵AE是⊙O切线;
∴∠EAB=∠ECA.
∵∠E=∠E,
∴△ABE∽△AEC.
∴
=
,
∴
=
②
∵AE是⊙O切线.
∴AE2=BE•EC③
由①②③得,
=
;
(3)∵⊙O直径为d
∴
=
,
∴
+
=2,
∴
+
=
.
 证明:(1)连接AB,OA,
证明:(1)连接AB,OA,∵弧AB=弧AF,OA是⊙O的半径,
∴OA⊥BF.
∵AE∥EF,
∴AE⊥OA.
∵OA是⊙O的半径,
∴AE是⊙O切线.
(2)∵BC是⊙O的直径,
∴∠BAC=90°.
∵AD⊥BC,
∴△ABD∽△ABC,△ACD∽△ABC.
∴AB2=BD•BC,AC2=CD•BC,
∴
| AB2 |
| AC2 |
| BD |
| CD |
∵AE是⊙O切线;
∴∠EAB=∠ECA.
∵∠E=∠E,
∴△ABE∽△AEC.
∴
| AB |
| AC |
| AE |
| EC |
∴
| AB2 |
| AC2 |
| AE2 |
| EC2 |
∵AE是⊙O切线.
∴AE2=BE•EC③
由①②③得,
| BD |
| CD |
| BE |
| EC |
(3)∵⊙O直径为d
∴
| d-CD |
| CD |
| EC-d |
| EC |
∴
| d |
| CD |
| d |
| EC |
∴
| 1 |
| CD |
| 1 |
| EC |
| 2 |
| d |
点评:此题考查了圆的切线的判定与性质、相似三角形的判定与性质以及比例式的变形等知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(2002•内江)如图,以Rt△BCF的斜边BC为直径作⊙O,A为 上一点,且
上一点,且 =
= ,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E.
,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E.
求证:
(1)AE是⊙O切线;
(2) ;
;
(3)若⊙O直径为d,则 .
.

 上一点,且
上一点,且 =
= ,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E.
,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E.求证:
(1)AE是⊙O切线;
(2)
 ;
;(3)若⊙O直径为d,则
 .
.
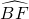 上一点,且
上一点,且 =
=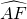 ,AD⊥BC,垂足为
,AD⊥BC,垂足为 D,过A作AE∥BF交CB的延长线于E.
D,过A作AE∥BF交CB的延长线于E.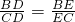 ;
;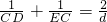 .
. 上一点,且
上一点,且 =
= ,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E.
,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E. ;
; .
.
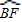 上一点,且
上一点,且 =
= ,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E.
,AD⊥BC,垂足为D,过A作AE∥BF交CB的延长线于E. ;
; .
.