题目内容
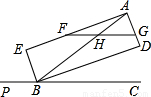
如图，BD、BE分别是∠ABC与它的邻补角∠ABP的平分线，AE⊥BE，AD⊥BD，E、D为垂足．
（1）求证：四边形AEBD是矩形；
（2）若
=3，F、G分别为AE、AD上的点，FG交AB于点H，且
=3，求证：△AHG是等腰三角形．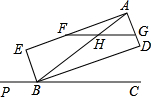
（1）求证：四边形AEBD是矩形；
（2）若
| AE |
| AD |
| AF |
| AG |
证明：（1）∵BD、BE分别是∠ABC与∠ABP的平分线，
∴∠ABD+∠ABE=
×180°=90°，
即∠EBD=90°，
又∵AE⊥BE，AD⊥BD，E、D是垂足，
∴∠AEB=∠ADB=90°，
∴四边形AEBD是矩形．
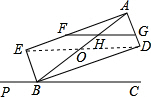
（2）连接ED交AB于O，
∵
=3，
=3，
∴
=
=3，
∴FG∥ED，
∴∠ADO=∠AGH，
∵四边形AEBD是矩形，
∴AB=DE，O是AB、DE的中点，
∴OD=OA，
∴∠ADO=∠DAO，
∴∠AGH=∠ADO=∠DAO，
∴AH=GH，
∴△AGH是等腰三角形．
∴∠ABD+∠ABE=
| 1 |
| 2 |
即∠EBD=90°，
又∵AE⊥BE，AD⊥BD，E、D是垂足，
∴∠AEB=∠ADB=90°，
∴四边形AEBD是矩形．
（2）连接ED交AB于O，
∵
| AE |
| AD |
| AF |
| AG |
∴
| AE |
| AD |
| AF |
| AG |
∴FG∥ED，
∴∠ADO=∠AGH，
∵四边形AEBD是矩形，
∴AB=DE，O是AB、DE的中点，
∴OD=OA，
∴∠ADO=∠DAO，
∴∠AGH=∠ADO=∠DAO，
∴AH=GH，
∴△AGH是等腰三角形．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
如图，BD、BE分别是∠ABC与它的邻补角∠ABP的平分线，AE⊥BE，AD⊥BD，E、D为垂足．
如图，BD，CD分别平分∠ABC和∠ACB，DE平行于BC交AC于点F，交AB于点E，若BC=4，BE=1.5，CF=1，则EF=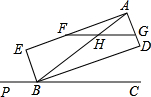
如图，BD、BE分别是∠ABC与它的邻补角∠ABP的平分线，AE⊥BE，AD⊥BD，E、D为垂足．
=3，F、G分别为AE、AD上的点，FG交AB于点H，且
=3，求证：△AHG是等腰三角形．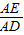
=3，F、G分别为AE、AD上的点，FG交AB于点H，且
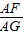=3，求证：△AHG是等腰三角形．