题目内容
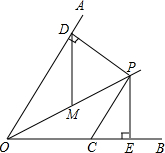 (2013•西宁)如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )
(2013•西宁)如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )分析:由OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,易得△OCP是等腰三角形,∠COP=30°,又由含30°角的直角三角形的性质,即可求得PE的值,继而求得OP的长,然后由直角三角形斜边上的中线等于斜边的一半,即可求得DM的长.
解答:解:∵OP平分∠AOB,∠AOB=60°,
∴∠AOP=∠COP=30°,
∵CP∥OA,
∴∠AOP=∠CPO,
∴∠COP=∠CPO,
∴OC=CP=2,
∵∠PCE=∠AOB=60°,PE⊥OB,
∴∠CPE=30°,
∴CE=
CP=1,
∴PE=
=
,
∴OP=2PE=2
,
∵PD⊥OA,点M是OP的中点,
∴DM=
OP=
.
故选C.
∴∠AOP=∠COP=30°,
∵CP∥OA,
∴∠AOP=∠CPO,
∴∠COP=∠CPO,
∴OC=CP=2,
∵∠PCE=∠AOB=60°,PE⊥OB,
∴∠CPE=30°,
∴CE=
| 1 |
| 2 |
∴PE=
| CP2-CE2 |
| 3 |
∴OP=2PE=2
| 3 |
∵PD⊥OA,点M是OP的中点,
∴DM=
| 1 |
| 2 |
| 3 |
故选C.
点评:此题考查了等腰三角形的性质与判定、含30°直角三角形的性质以及直角三角形斜边的中线的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
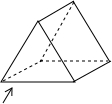 (2013•西宁)如图所示的几何体的俯视图应该是( )
(2013•西宁)如图所示的几何体的俯视图应该是( ) (2013•西宁)如图,矩形的长和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合.设矩形与等腰三角形重叠部分(阴影部分)的面积为y,重叠部分图形的高为x,那么y关于x的函数图象大致应为( )
(2013•西宁)如图,矩形的长和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合.设矩形与等腰三角形重叠部分(阴影部分)的面积为y,重叠部分图形的高为x,那么y关于x的函数图象大致应为( )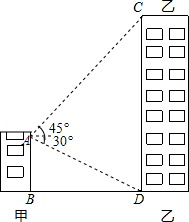 (2013•西宁)如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为
(2013•西宁)如图,甲乙两幢楼之间的距离是30米,自甲楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°,则乙楼的高度为 (2013•西宁)如图,网格图中每个小正方形的边长为1,则弧AB的弧长l=
(2013•西宁)如图,网格图中每个小正方形的边长为1,则弧AB的弧长l=