Question

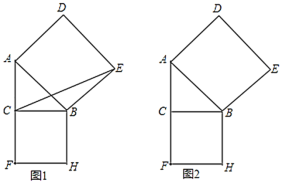
【题目】在中，，分别以，为边向外作正方形和正方形．

（1）当时，正方形的周长=_______（用含的代数式表示）；

（2）连接．试说明：三角形的面积等于正方形面积的一半．

（3）已知，且点是线段上的动点，点是线段上的动点，当点和点在移动过程中，的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

Answer 1

【答案】（1）4m；（2）证明见解析；（3）△APQ的周长的最小值为4．

【解析】

（1）直接由正方形的性质得出答案即可；

（2）连接AH，证明△BHA≌△BCE，利用△BHA的面积=△BCE的面积得出结论；

（3）作点A关于DE的对称点A′，点A关于BC的对称点F，利用对称的性质得出△APQ的周长的最小值为A′F，进一步求得问题即可．

（1）∵四边形BCFH是正方形，

∴BC=BH=FH=CF，

∴当BC=m时，正方形BCFH的周长为4m，

故答案为：4m；

（2）如图1，连接AH，

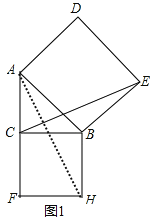
在△BHA和△BCE中，

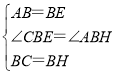
∴△BHA≌△BCE（SAS），

∵AF∥BH，

∴BH边上的高=正方形BCFH的边

∴△BHA的面积等于正方形BCFH的面积．

∴△AEC的面积等于正方形BCFH的面积；

（3）△APQ的周长存在最小值．

如图2，作点A关于DE的对称点A

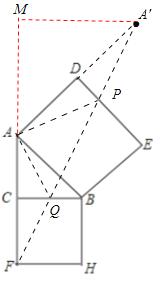
∴AP=A′P

∵点A关于BC的对称点F，

∴AQ=QF，

∴△APQ的周长的最小值为A′F，

过A′作A′M⊥FA交FA的延长线于M，

∵，

∴∠BAC=45°，AB=2

∴∠A′AM=45°, AA′=4，

∴△AA′M为等腰直角三角形，，

∴MA=MA′=4，

∴MF=8，

∴A′F==4，

∴△APQ的周长的最小值为4．