Question

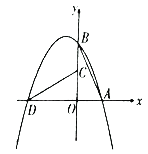
【题目】如图，在平面直角坐标系中，抛物线经过，两点.将绕点逆时针旋转90°得到，点在抛物线上.

（1）求该抛物线的表达式；

（2）已知点在轴上（点不与点重合），连接，若与相似，试求点的坐标。

Answer 1

【答案】（1）；（2）点的坐标为或或.

【解析】

（1）由旋转的性质求出D的坐标，再由待定系数法可得出函数关系式；

（2）设点M的坐标为（0，m），由ΔAOB与ΔAOM相似，且∠AOB=∠AOM=90°，分两种情况讨论即可．

（1）由旋转可得OD=OB=4，则D（-4，0）．由抛物线经过B（0，4），可设y=ax2+bx+4，代入A（2，0），D（-4，0）可得：，解得：．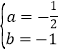

因此该抛物线的表达式为．

（2）由题可知OA=2，OB=4，设点M的坐标为（0，m），如图．

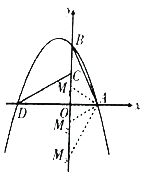
∵ΔAOB与ΔAOM相似，且∠AOB=∠AOM=90°，∴分两种情况讨论：

①若，即，∴|m|=4，即m=±4．

∵点M不与点C重合，∴m=-4，此时点M的坐标为M1 （0，-4）．

②若，即，∴|m|=1，即m=±1．

此时点M的坐标为M2 （0，-1）或M3 （0，1）．

综上所述：点M的坐标为M1 （0，-4）或M2 （0，-1）或M3 （0，1）．