题目内容
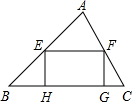 如图,△ABC面积为48,E,F分别为AB,AC中点,则矩形EFGH的面积为
如图,△ABC面积为48,E,F分别为AB,AC中点,则矩形EFGH的面积为24
24
.分析:先判定EF是△ABC的中位线,然后根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=
BC,过点A作AM⊥BC交EF于点N,交BC于M,然后根据相似三角形对应高线的比等于相似比求出MN的长,最后求出矩形的面积等于△ABC面积的一半.
| 1 |
| 2 |
解答: 解:∵E,F分别为AB,AC中点,
解:∵E,F分别为AB,AC中点,
∴EF∥BC,EF=
BC,
∴△AEF∽△ABC,
过点A作AM⊥BC交EF于点N,交BC于M,
∴
=
,
即
=
,
解得MN=
AM,
∴矩形EFGH的面积=EF•MN=
BC•
AM=
(
BC•AM)=
S△ABC,
∵△ABC面积为48,
∴矩形EFGH的面积为
×48=24.
故答案为:24.
 解:∵E,F分别为AB,AC中点,
解:∵E,F分别为AB,AC中点,∴EF∥BC,EF=
| 1 |
| 2 |
∴△AEF∽△ABC,
过点A作AM⊥BC交EF于点N,交BC于M,
∴
| AN |
| AM |
| EF |
| BC |
即
| AM-MN |
| AM |
| 1 |
| 2 |
解得MN=
| 1 |
| 2 |
∴矩形EFGH的面积=EF•MN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC面积为48,
∴矩形EFGH的面积为
| 1 |
| 2 |
故答案为:24.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,矩形的性质,相似三角形对应高的比等于相似比,求出矩形的宽等于△ABC的BC边上的高的一半是解题的关键.

练习册系列答案
相关题目
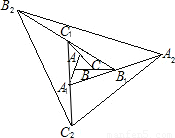
 11、如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2006,最少经过
11、如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2006,最少经过
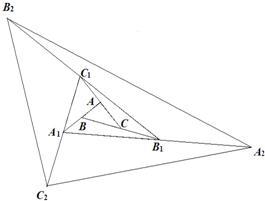
 10、如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过_____次操作( )
10、如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过_____次操作( ) 如图,△ABC面积为1,
如图,△ABC面积为1,