题目内容
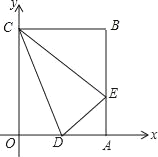
【题目】如图,抛物线![]() 与x轴分别交于点
与x轴分别交于点![]() ,与y轴交于点C,顶点为D.
,与y轴交于点C,顶点为D.
(1)求抛物线的解析式和顶点D的坐标;
(2)动点![]() 以相同的速度从点O同时出发,分别在线段
以相同的速度从点O同时出发,分别在线段![]() 上向点
上向点![]() 方向运动,过点P作x轴的垂线,交抛物线于点E.
方向运动,过点P作x轴的垂线,交抛物线于点E.
①当四边形![]() 为矩形时,求点E的坐标;
为矩形时,求点E的坐标;
②过点E作![]() 于点M,连接
于点M,连接![]() .设
.设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,当
,当![]() 将
将![]() 的面积分成1:3两部分时,请直接写出的
的面积分成1:3两部分时,请直接写出的![]() 值;
值;
③连接![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
【答案】(1)![]() ;
;![]() ;(2)①
;(2)①![]() ;②15或
;②15或![]() ;③
;③![]()
【解析】
(1)将点A、B代入抛物线解析式即可,则点D坐标可求.
(2)①四边形为矩形,可分析出OQ=PE,设点坐标表示线段长度列式求解即可.
②PE分三角形的面积之比为1:3,可分析出PE分线段BC为1:3,分两种情况讨论,分别求出S1和S2,则比值可求.
③转化线段CP为线段BQ,作点D关于y轴的对称点,连接BD′,与y轴的交点即为点Q,求出BD′的长度就是CP+DQ的最小值.
解:(1)将点A、B代入解析式
![]()
解得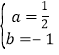 ,
,
∴y=![]() -x-4
-x-4
当x=1时,y=-![]() ,
,
∴D(1,-![]() ).
).
(2)①设点E的坐标为(m,![]() -m-4),则点P(m,0),点Q(0,-m),
-m-4),则点P(m,0),点Q(0,-m),
∵四边形OQEP为矩形,
∴OQ=EP,
∴m=-![]() +m+4,
+m+4,
解得![]() =-2
=-2![]() (舍去),m2=2
(舍去),m2=2![]() .
.
∴E(2![]() , -2
, -2![]()
②令x=0,y=-4,
∴C(0,-4),
∵PE将△BCE的面积分成1:3两部分,
∴PE将线段BC分成1:3两部分,
情况一:当PE过靠近点C的四等分点时,点P的坐标为(1,0),点E(1,-![]() ),
),
∴点Q(0,-1),
直线BC的解析式为y=x-4,
当x=1时,y=-3,
∴点G(1,-3),
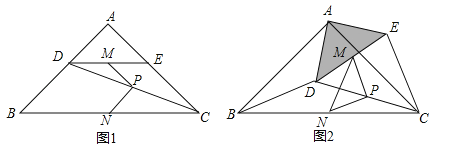
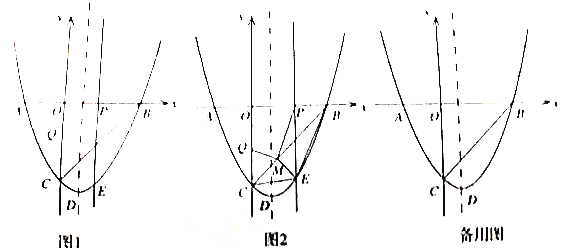
如图1所示,

∴GD=![]() ,
,
∵∠CGD=∠OBC=45°,
∴xM=1-![]() ,
,
∴M(![]() ),
),
∴S1=3![]()
![]() =
=![]() , S2=3
, S2=3![]()
![]() =
=![]() ,
,
∴![]() =15.
=15.
情况二:当PE过靠近点B的四等分点时,点P(3,0),点Q(0,-3),点E(3,-![]() ),点G(3,-1),
),点G(3,-1),
∴EG=![]() ,
,
∴xM=3-![]() ,
,
∴M(![]() ,-
,-![]() ),
),
∴S1=1![]()
![]() =
=![]() , S2=1
, S2=1![]()
![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
综上所述:![]() =15或
=15或![]() =
=![]() .
.
③如图2所示,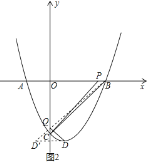
∵OP=OQ,∠BOQ=∠COP,OB=OC,
∴△BOQ≌△COP(SAS),
∴CP=BQ,
∴CP+DQ=BQ+DQ,
作点D关于y轴的对称点D′(-1,-![]() ),
),
连接BD′,与y轴的交点即为点Q,
BD′=![]() =
=![]() .
.
∴CP+DQ的最小值为![]() .
.

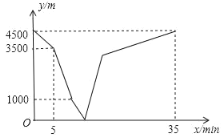
【题目】大学生小亮响应国家创新创业号召,回家乡承包了一片坡地,改造后种植优质猕猴桃.经核算这批猕猴桃的种植成本为16 元![]() ,设销售时间为
,设销售时间为![]() (天),通过一个月(30天)的试销得出如下规律:①猕猴桃的销售价格p(元
(天),通过一个月(30天)的试销得出如下规律:①猕猴桃的销售价格p(元![]() )与时间x(天)的关系:当
)与时间x(天)的关系:当![]() 时,p与x满足一次函数关系,如下表:
时,p与x满足一次函数关系,如下表:
| 2 | 4 | 6 | ...... |
| 35 | 34 | 33 | ...... |
当![]() 时,销售价格稳定为24元
时,销售价格稳定为24元![]() ;②猕猴桃的销售量
;②猕猴桃的销售量![]() 与时间
与时间![]() (天)之间的关系:第一天卖出
(天)之间的关系:第一天卖出![]() ,以后每天比前一天多卖出
,以后每天比前一天多卖出![]() .
.
(1)填空:试销的一个月中,销售价p(元![]() )与时间
)与时间![]() (天)的函数关系式为____;销售量
(天)的函数关系式为____;销售量![]() 与时间x(天)的函数关系式为_____.
与时间x(天)的函数关系式为_____.
2)求销售第几天时,当天的利润最大?最大利润是多少?
(3)请求出试销的一个月中当天销售利润不低于 930 元的天数.
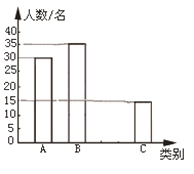
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?