题目内容
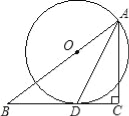
【题目】如图,在⊙O中,AB是直径, CD是弦,AB⊥CD。
(1)P是优弧CAD上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P在劣弧CD上(不与C、D重合)时,∠CPD与∠COB数量关系是什么?(直接写出答案)

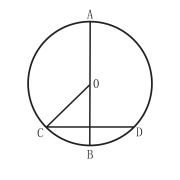
【答案】(1)、证明过程见解析;(2)、∠CPD+∠COB=180°
【解析】
试题分析:(1)、连接OD,根据垂径定理可得:∠COB=∠DOB=![]() ∠COD,结合∠CPD=
∠COD,结合∠CPD=![]() ∠COD,从而得出∠CPD=∠COB;(2)、根据题意得出答案.
∠COD,从而得出∠CPD=∠COB;(2)、根据题意得出答案.
试题解析:(1)、连接OD, ∵AB是直径,AB⊥CD, ∴∠COB=∠DOB=![]() ∠COD
∠COD
又∵∠CPD=![]() ∠COD, ∴∠CPD=∠COB。
∠COD, ∴∠CPD=∠COB。
(2)、∠CPD与∠COB的数量关系是:∠CPD+∠COB=180°

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目