题目内容
 有两棵树,一棵高5米,另一棵高2米,两树相距5米,一只小鸟从一棵树的树梢的顶端飞到另一棵树的树梢的顶端,至少飞了
有两棵树,一棵高5米,另一棵高2米,两树相距5米,一只小鸟从一棵树的树梢的顶端飞到另一棵树的树梢的顶端,至少飞了分析:根据“两点之间线段最短”可知:小鸟沿着两棵树的树尖进行直线飞行,所行的路程最短,运用勾股定理可将两点之间的距离求出.
解答:解:两棵树的高度差为5-2=3m,间距为5m,
根据勾股定理可得:小鸟至少飞行的距离=
=
m.
故答案为:
.
根据勾股定理可得:小鸟至少飞行的距离=
| 52+32 |
| 34 |
故答案为:
| 34 |
点评:本题主要考查了勾股定理的应用,解题的关键是将现实问题建立数学模型,运用数学知识进行求解.

练习册系列答案
相关题目

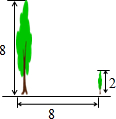 如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一
如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一 如图、有两棵树,一棵高6米,另一棵高2米,两树相距5米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了( )米.
如图、有两棵树,一棵高6米,另一棵高2米,两树相距5米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了( )米.