Question

【题目】如图,已知OA,OB是☉O的半径,C为的中点,M,N分别是OA,OB的中点,求证:MC=NC.

Answer 1

【答案】证明见解析

【解析】试题分析: 连接OC，根据C是的中点，易得到，由同圆中等弧对的圆心角相等可得∠AOC=∠BOC；由OA=OB，M，N分别为OA，OB的中点可得OM=ON，由边角边定理可以判断△MOC≌△NOC，从而可得到MC=NC.

证明:连接OC.

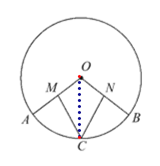
∵C为的中点,∴=,

∴∠MOC=∠NOC.

又∵M,N分别是OA,OB的中点,

∴OM=OA,ON=OB,

∴OM=ON.

又∵OC=OC,

∴△OMC≌△ONC,∴MC=NC.

点睛:本题考查三角形全等的判定方法,弧与圆心角之间的关系，解题的关键是灵活运用三角形全等的判定方法及在等圆或同圆中相等的弧所对的圆心角相等这些定理；