题目内容
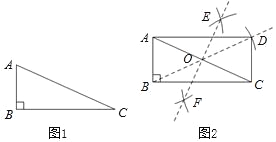
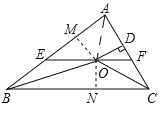
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() 下列结论:①
下列结论:①![]() ;②点
;②点![]() 到
到![]() 各边的距离相等;③
各边的距离相等;③![]() ;④设
;④设![]() ,
,![]() ,则
,则![]() ;⑤
;⑤![]() .其中正确的结论是.__________.
.其中正确的结论是.__________.

【答案】①②③⑤
【解析】
由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得③∠BOC=90°+![]() ∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD=m,AE+AF=n,则S△AEF=
∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD=m,AE+AF=n,则S△AEF=![]() mn,故④错误,根据HL证明△AMO≌△ADO得到AM=AD,同理可证BM=BN,CD=CN,变形即可得到⑤正确.
mn,故④错误,根据HL证明△AMO≌△ADO得到AM=AD,同理可证BM=BN,CD=CN,变形即可得到⑤正确.
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣
∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣![]() ∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+
∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+![]() ∠A;故③正确;
∠A;故③正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF.
∵EF∥BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA.
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=![]() AEOM+
AEOM+![]() AFOD=
AFOD=![]() OD(AE+AF)=
OD(AE+AF)=![]() mn;故④错误;
mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到△ABC各边的距离相等,故②正确;
∵AO=AO,MO=DO,∴△AMO≌△ADO(HL),∴AM=AD;
同理可证:BM=BN,CD=CN.
∵AM+BM=AB,AD+CD=AC,BN+CN=BC,∴AD=![]() (AB+AC﹣BC)故⑤正确.
(AB+AC﹣BC)故⑤正确.
故答案为:①②③⑤.

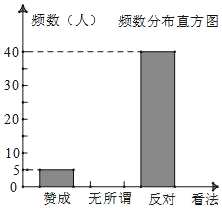
【题目】校园手机现象已经受到社会的广泛关注.某校的一个兴趣小组对“是否赞成中学生带手机进校园”的问题在该校校园内进行了随机调查.并将调查数据作出如下不完整的整理;
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |
(1)本次调查共调查了 人;(直接填空)
(2)请把整理的不完整图表补充完整;
(3)若该校有3000名学生,请您估计该校持“反对”态度的学生人数.