题目内容
【题目】如图,ABC中,AB=AC=4![]() ,cosC=
,cosC=![]() .
.
(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法).
(2)综合应用:在你所作的圆中,求证: ![]() ;
;
(3)求△BDE的周长.
【答案】(1)作图见解析;(2)证明见解析;(3)△BDE的周长为8+![]() .
.
【解析】试题分析:做AC的中垂线得出圆心的位置;(2)连接AE,根据直径的性质得出∠AEC=∠AEB=90°,根据AB=AC得出∠BAE=∠CAE,从而得出∠CAE=∠BAE,得出弧相等;(3)根据Rt△ACE的三角形函数得出CE的长度,根据(2)得出BE=CE=DE=4,根据Rt△BCD中∠B的三角函数得出BC和BD的长度,从而得出三角形周长.
试题解析:(1)如图1,⊙O为所求.
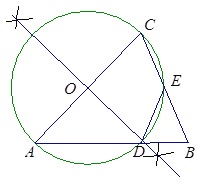
(2)证明:如图,连接AE, ∵AC为⊙O的直径,点E在⊙O上,∴∠AEC=90°,
∵AB=AC,∴∠BAE =∠CAE, ∴![]() .
.
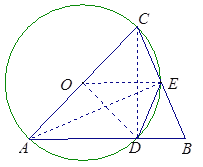
(3)解:如图在Rt△ACE中,
![]() ,
, ![]() ,∴
,∴![]() .
.
∵AB= AC,∠AEC=90°,∴∠B =∠ACB,BE= CE=4. 又![]()
![]() ,∴DE= CE=4.
,∴DE= CE=4.
在Rt△BCD中, ![]() , ∵
, ∵![]() ,BC=8,
,BC=8,
∴![]() ,
,
∴![]() 的周长
的周长![]()
![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目