题目内容
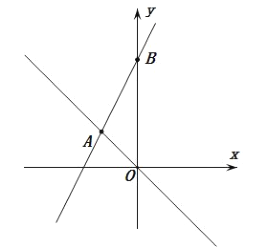
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)在平面直角坐标系中有一点![]() ,若
,若![]() ,则
,则![]() 与
与![]() 满足的关系式是什么?
满足的关系式是什么?
(3)已知平行于![]() 轴且位于
轴且位于![]() 轴左侧有一动直线,分别与
轴左侧有一动直线,分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() 且点
且点![]() 在点
在点![]() 的下方,点
的下方,点![]() 为
为![]() 轴上一动点,且
轴上一动点,且![]() 为等腰直角三角形,请直接写出满足条件的点
为等腰直角三角形,请直接写出满足条件的点![]() 的坐标.
的坐标.
【答案】(1)![]() 的解析式为
的解析式为![]() ;(2) m+n=3或m+n=-3;(3)
;(2) m+n=3或m+n=-3;(3) ![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ).
).
【解析】
(1)可得A(-1,1)B(0,3),设![]() 的解析式为
的解析式为![]() ,代入A(-1,1),可得
,代入A(-1,1),可得![]() 的解析式;
的解析式;
(2)①当点P在![]() 的右侧时,设点P为
的右侧时,设点P为![]() ,且
,且![]() B//
B//![]() ,
,![]() B的解析式为:y=-x+3,即:n=-m+3,m+n=3,②当点P
B的解析式为:y=-x+3,即:n=-m+3,m+n=3,②当点P![]() 在的左侧时,设点P为
在的左侧时,设点P为![]() ,,,可得B点关于O点的对称点位
,,,可得B点关于O点的对称点位![]() (0,-3)点在
(0,-3)点在![]() ;
;![]() 上,且
上,且![]()
![]() //
//![]() ,
,![]()
![]() 的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
(3)设动直线为x=t,由题可得-1<t<0,则M(t,-t),N(t,2t+3),MN=3t+3,
当NM⊥NQ且NM=NQ时,Q(0,2t+3),由3t+3=-t,t=-![]() ,可得Q的值,
,可得Q的值,
当MN⊥MQ且NM=MQ时,Q(0,-t),由3t+3=-t,t=-![]() ,可得Q的值,
,可得Q的值,
当QN⊥QM且QN=QM时,Q(0,![]() ),可得2t+3-(
),可得2t+3-(![]() )=-t,解得t=
)=-t,解得t=![]() ,可得Q的值.
,可得Q的值.
解:(1)由题可得: a=-1,b=3
则点A(-1,1)B(0,3)
设![]() 的解析式为
的解析式为![]() ,代入A(-1,1)得:1=-k+3,
,代入A(-1,1)得:1=-k+3,
解得:k=2,
![]()
![]() 的解析式为
的解析式为![]()
(2)![]() ,则点P到AO的距离与点B到AO的距离相等,且点P位于h两侧;
,则点P到AO的距离与点B到AO的距离相等,且点P位于h两侧;
①当点P在![]() 的右侧时,设点P为
的右侧时,设点P为![]() ,且
,且![]() B//
B//![]()
![]()
![]() B的解析式为:y=-x+3,即:n=-m+3,m+n=3
B的解析式为:y=-x+3,即:n=-m+3,m+n=3
②当点P![]() 在的左侧时,设点P为
在的左侧时,设点P为![]() ,,
,,
可得B点关于O点的对称点位![]() (0,-3)点在
(0,-3)点在![]() ;
;![]() 上,且
上,且![]()
![]() //
//![]() ,
,
![]()
![]()
![]() 的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
综合:m+n=3或m+n=-3;
(3)设动直线为x=t,由题可得-1<t<0,
则M(t,-t),N(t,2t+3),MN=3t+3,
当NM⊥NQ且NM=NQ时,Q(0,2t+3),由3t+3=-t,t=-![]() ,此时
,此时![]() (0,
(0,![]() )
)
当MN⊥MQ且NM=MQ时,Q(0,-t),由3t+3=-t,t=-![]() ,此时
,此时![]() (0,
(0,![]() )
)
当QN⊥QM且QN=QM时,Q(0,![]() ),可得2t+3-(
),可得2t+3-(![]() )=-t,解得t=
)=-t,解得t=![]() ,此时
,此时![]() (0,
(0,![]() ),
),
综上![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ).
).

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术饰品 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
【题目】在我校“书香校园”活动中,某数学小组为了解学生家庭藏书情况,随机抽取我校部分学生进行调查,并绘制成部分统计图如下表:
类别 | 家庭藏书情况统计表 | 学生人数 |
|
| 20 |
|
|
|
|
| 50 |
|
| 66 |
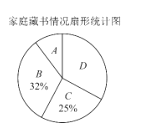
根据以上信息,解答下列问题:
(1)参加调查的学生人数为多少,a等于多少,本次调查结果的中位数在哪一类.
(2)在扇形统计图中,“![]() ”对应扇形的圆心角为多少.
”对应扇形的圆心角为多少.
(3)若我校有4500名学生,请估计全校学生中藏书200本以上的人数.