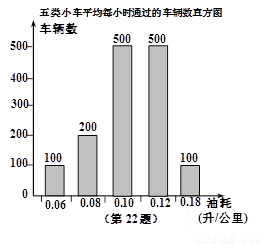题目内容
(本题满分9分)下表是甲地到乙地两条线路的有关数据:
| 线路 | 绕路 | 直路 |
| 路程 | 300公里 | 180公里 |
| 过路费 | 30元 | 90元 |
(2)若小车每公里的油耗为
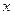 升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
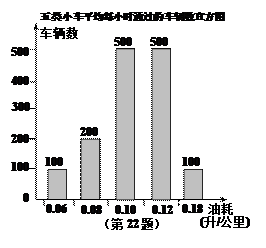
升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);(3)据道路管理部门统计:得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数,制成如图所示的频数分布直方图,请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油.
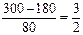 ,………………………………………………………2分
,………………………………………………………2分 (2)y1=7.5×300x+30=2250 x+30,
y2=7.5×180x+90=1350x+90,……………………………………………………………4分
① 若y1=y2,解得
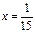 ;走两种路的费用相同;
;走两种路的费用相同;②若y1>y2,即当x>
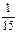 时,走直路费用较少;
时,走直路费用较少;③若y1<y2,即当x<
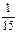 ,走弯路费用较少.…………………………………………………7分
,走弯路费用较少.…………………………………………………7分(3)10×120×(100×0.06+200×0.08+500×0.1+500×0.12+100×0.18)=180000(升).…9分解析:
略

 作业辅导系列答案
作业辅导系列答案(本题满分12分)
问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为![]() .
.
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数![]() 的图象性质.
的图象性质.
① 填写下表,画出函数的图象:
| x | … |
|
|
| 1 | 2 | 3 | 4 | … |
| y | … |
|
|
|
|
|
|
| … |
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数![]() (x>0)的最小值.
(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.

(本题满分9分)
下表是甲地到乙地两条线路的有关数据:
| 线路 | 绕路 | 直路 |
| 路程 | 300公里 | 180公里 |
| 过路费 | 30元 | 90元 |
(1)若小车的平均速度为80公里/小时,则小车走直路比走弯路节省多少时间?
(2)若小车每公里的油耗为![]() 升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
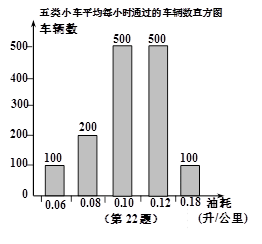
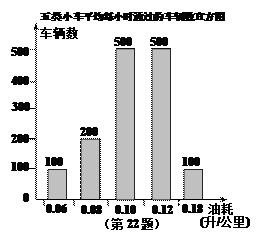
(3)据道路管理部门统计:得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数,制成如图所示的频数分布直方图,请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油.
(本题满分9分)
下表是甲地到乙地两条线路的有关数据:
| 线路 | 绕路 | 直路 |
| 路程 | 300公里 | 180公里 |
| 过路费 | 30元 | 90元 |
(2)若小车每公里的油耗为
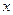 升,按汽油价格为7.5元/升计算,
升,按汽油价格为7.5元/升计算, 设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);(3)据道路管理部门统计:得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数,制成如图所示的频数分布直方图,请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油.
(本题满分9分)
下表是甲地到乙地两条线路的有关数据:
|
线路 |
绕路 |
直路 |
|
路程 |
300公里 |
180公里 |
|
过路费 |
30元 |
90元 |
(1)若小车的平均速度为80公里/小时,则小车走直路比走弯路节省多少时间?
(2)若小车每公里的油耗为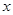 升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
升,按汽油价格为7.5元/升计算,设走弯路的总费用为y1,走直路的总费用为y2,问x为何值时,所走哪条线路的总费用较少(总费用=过路费+油耗费);
(3)据道路管理部门统计:得到从甲地到乙地的五类不同油耗的小车平均每小时通过的车辆数,制成如图所示的频数分布直方图,请你估算每天早晨7点至晚上5点内这五类小车走直路比走弯路共节省多少升汽油.