题目内容
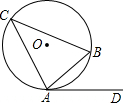已知如图，AB为⊙O的弦，C为⊙O上一点，∠C=∠BAD．求证：AD是⊙O的切线．
证明：作直径AM，连接BM，则∠M+∠MAB=90°，
∵∠M=∠C=∠BAD，
∴∠BAD+∠BAM=90°，
∴OA⊥AD
∴AD是⊙O的切线．
分析：作直径AM，连接BM，要证明AD是⊙O的切线只要证明∠OAD=90°即可．
点评：本题利用了直径对的圆周角是直角，圆周角定理，切线的概念及判定的知识，知识点比较多，但题目难度不大．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
21、已知如图，AB为⊙O的弦，C为⊙O上一点，∠C=∠BAD．求证：AD是⊙O的切线．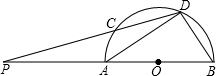
已知如图，AB为半圆的直径，C、D为半圆弧上的两点，若弧CD=弧BD，DC与BA的延长线交于P，如果，AP：CP=3：4，△ADB的面积为
