题目内容
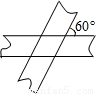
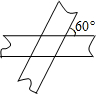
 如图,两条宽度为1的纸带,相交成60°角,那么重叠部分的面积是________.
如图,两条宽度为1的纸带,相交成60°角,那么重叠部分的面积是________.

分析:根据题意可知:所得图形是菱形,设菱形ABCD,由已知得∠B=60°,过A作AE⊥BC于E,由勾股定理可求BE、AB、BC的长度,根据菱形的面积公式即可求出所填答案.
解答:
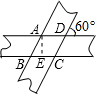 解:由题意可知:重叠部分是菱形,设菱形ABCD,则∠B=60°,
解:由题意可知:重叠部分是菱形,设菱形ABCD,则∠B=60°,过A作AE⊥BC于E,则AE=1,
设BE=x,
∵∠B=60°,
∴∠BAE=30°,
∴AB=2x,
在△ABE中,∠AEB=90°,由勾股定理并解得:
x=
 ,
,∴AB=BC=
 ,
,∴重叠部分的面积是:
 ×1=
×1= .
.故答案为:

点评:本题主要考查了菱形的性质,勾股定理,含30°角的直角三角形的性质,菱形的面积公式等知识点,把实际问题转化成数学问题,利用所学的知识进行计算是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
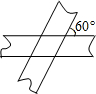
 如图,两条宽度为1的纸带,相交成60°角,那么重叠部分的面积是
如图,两条宽度为1的纸带,相交成60°角,那么重叠部分的面积是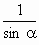
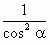


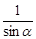 B、
B、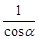 C、sinα
D、1
C、sinα
D、1