题目内容
如图,已知C,D是双曲线y=| m |
| x |
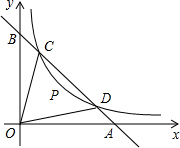 ,D(x2,y2),连接OC,OD(O是坐标原点),若∠BOC=∠AOD=α,且tanα=
,D(x2,y2),连接OC,OD(O是坐标原点),若∠BOC=∠AOD=α,且tanα=| 1 |
| 3 |
| 10 |
(1)求C,D的坐标和m的值;
(2)双曲线存在一点P,使得△POC和△POD的面积相等,求点P的坐标;
(3)在(2)的条件下判断点P是否为△OCD的重心.
(4)已知点Q(-2,0),问在直线AC上是否存在一点M使△MOQ的周长L取得最短?若存在,求出L的最小值并证明;若不存在,请说明理由.
分析:(1)过点C作CG⊥x轴于G,在直角△OCG中,已知tanα=
,OC=
,就可以求出CG,OQ的长,就得到C点的坐标.根据待定系数法得到反比例函数的解析式.过D作DH⊥y轴于H,则DH=y2,OH=x2,在Rt△ODH中,tanα=
=
,∴
=
,即y2=3x2,由x2y2=3解得DH的长,进而求出OH,得到D点的坐标.
(2)双曲线上存在点P,使得S△POC=S△POD,这个点就是∠COD的平分线与双曲线的y=
交点,易证△POC≌△POD,则S△POC=S△POD.
(3)根据点P到三个顶点的距离即可判断是否为三角形△OCD的重心;
(4)先求出直线CD的解析式,表示出△MOQ的周长L,根据配方法即可求解.
| 1 |
| 3 |
| 10 |
| DH |
| OH |
| 1 |
| 3 |
| x2 |
| y2 |
| 1 |
| 3 |
(2)双曲线上存在点P,使得S△POC=S△POD,这个点就是∠COD的平分线与双曲线的y=
| 3 |
| x |
(3)根据点P到三个顶点的距离即可判断是否为三角形△OCD的重心;
(4)先求出直线CD的解析式,表示出△MOQ的周长L,根据配方法即可求解.
解答:解:(1)过点C作CG⊥x轴于G,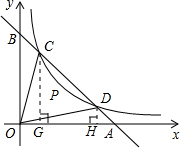
则CG=y1,OG=x1,
在Rt△OCG中,∠GCO=∠BOC=α,
∵tanα=
=
,
∴
=
,
即y1=3x1,
又∵OC=
,
∴x12+y12=10,
即x12+(3x1)2=10,
解得:x1=1或x1=-1(不合舍去)
∴x1=1,y1=3,
∴点C的坐标为C(1,3).
又点C在双曲线上,可得:m=3,
过D作DH⊥y轴于H,则DH=y2,OH=x2
在Rt△ODH中,tanα=
=
,
∴
=
,
即y2=3x2,
又∵x2y2=3,
∴y2=1或y2=-1(不符合舍去),
∴x2=3,y2=1,
∴点D的坐标为D(3,1);
(2)双曲线上存在点P,使得S△POC=S△POD,
这个点就是∠COD的平分线与双曲线的y=
交点,
故P点坐标为(
,
),
∵点D(3,1),
∴OD=
,
∴OD=OC,
∴点P在∠COD的平分线上,
则∠COP=∠POD,又OP=OP
∴△POC≌△POD,
∴S△POC=S△POD.
(3)延长OP交CD于M,
∵C(1,3),D(3,1),
∴根据勾股定理OC=OD=
,
∵点P在∠COD的平分线上,
∴M为CD中点,
∴M(2.,2),
∵P点坐标为(
,
),
∴OP=
,PM=
=-
+2
即OP≠2PM,
∴P不是△OCD的重心.
(4)∵点C的坐标为C(1,3),点D的坐标为D(3,1),
设直线CD的解析式为y=kx+b.
则有
,解得
.
∴直线CD的解析式为y=-x+4,
∵Q(-2,0),假设存在M(a,-a+4),则点M关于x轴的对称点M′为(a,4-a),
∴△MOQ的周长L=2+
=2+
,
所以当a=1时,周长L取最小值为2+3
,
此时点M(1,3),故L取最小值为2+3
.

则CG=y1,OG=x1,
在Rt△OCG中,∠GCO=∠BOC=α,
∵tanα=
| OG |
| CG |
| 1 |
| 3 |
∴
| x2 |
| x1 |
| 1 |
| 3 |
即y1=3x1,
又∵OC=
| 10 |
∴x12+y12=10,
即x12+(3x1)2=10,
解得:x1=1或x1=-1(不合舍去)
∴x1=1,y1=3,
∴点C的坐标为C(1,3).
又点C在双曲线上,可得:m=3,
过D作DH⊥y轴于H,则DH=y2,OH=x2
在Rt△ODH中,tanα=
| DH |
| OH |
| 1 |
| 3 |
∴
| x2 |
| y2 |
| 1 |
| 3 |
即y2=3x2,
又∵x2y2=3,
∴y2=1或y2=-1(不符合舍去),
∴x2=3,y2=1,
∴点D的坐标为D(3,1);
(2)双曲线上存在点P,使得S△POC=S△POD,

这个点就是∠COD的平分线与双曲线的y=
| 3 |
| x |
故P点坐标为(
| 3 |
| 3 |
∵点D(3,1),
∴OD=
| 10 |
∴OD=OC,
∴点P在∠COD的平分线上,
则∠COP=∠POD,又OP=OP
∴△POC≌△POD,
∴S△POC=S△POD.
(3)延长OP交CD于M,
∵C(1,3),D(3,1),
∴根据勾股定理OC=OD=
| 10 |
∵点P在∠COD的平分线上,
∴M为CD中点,
∴M(2.,2),
∵P点坐标为(
| 3 |
| 3 |
∴OP=
| 6 |
(
|
| 6 |
| 2 |
即OP≠2PM,
∴P不是△OCD的重心.
(4)∵点C的坐标为C(1,3),点D的坐标为D(3,1),
设直线CD的解析式为y=kx+b.
则有
|
|
∴直线CD的解析式为y=-x+4,
∵Q(-2,0),假设存在M(a,-a+4),则点M关于x轴的对称点M′为(a,4-a),
∴△MOQ的周长L=2+
| 2a2-4a+20 |
=2+
| 2(a-1)2+18 |
所以当a=1时,周长L取最小值为2+3
| 2 |
此时点M(1,3),故L取最小值为2+3
| 2 |
点评:本题考查了解直角三角形及三角形的重心等知识,难度较大,关键是掌握用待定系数法求函数解析式及角平分线的性质.

练习册系列答案
相关题目
 最低成本是
最低成本是
 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求: 著名数学教育家G.波利亚,有句名言:“发现问题比解决问题更重要”,这句话启发我们:要想学好数学,就需要观察,发现问题,探索问题的规律性东西,要有一双敏锐的眼睛.请先观察、计算再填空.
著名数学教育家G.波利亚,有句名言:“发现问题比解决问题更重要”,这句话启发我们:要想学好数学,就需要观察,发现问题,探索问题的规律性东西,要有一双敏锐的眼睛.请先观察、计算再填空.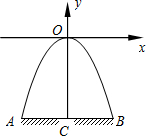 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求: