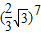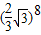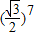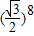题目内容
先作半径为 的第一个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,…,则按以上规律作出的第8个外切正六边形的边长为
的第一个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,…,则按以上规律作出的第8个外切正六边形的边长为
- A.
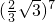
- B.
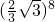
- C.
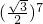
- D.
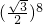
A
分析:先求出第一个正六边形的边长,再求第二个,依此规律找到第七个.
解答:每个正六边形都相似,且相邻的两个正六边形的相似比就是正六边形的半径与边心距的比,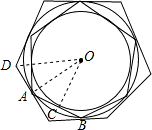
即 =
=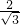 =
= ,
,
第一个正六边形的边长是1,
则第二个的边长是1× ,
,
第三个的边长为( )
)
第八个是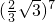 .
.
故选A.
点评:正多边形的计算一般是通过中心作边的垂线,连接半径,把正多边形中的半径,边长,边心距,中心角之间的计算转化为解直角三角形.
分析:先求出第一个正六边形的边长,再求第二个,依此规律找到第七个.
解答:每个正六边形都相似,且相邻的两个正六边形的相似比就是正六边形的半径与边心距的比,

即
 =
=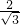 =
= ,
,第一个正六边形的边长是1,
则第二个的边长是1×
 ,
,第三个的边长为(
 )
)第八个是
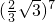 .
.故选A.
点评:正多边形的计算一般是通过中心作边的垂线,连接半径,把正多边形中的半径,边长,边心距,中心角之间的计算转化为解直角三角形.

练习册系列答案
相关题目
先作半径为
的第一个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,…,则按以上规律作出的第8个外切正六边形的边长为( )
| ||
| 2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
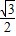 的第一个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,…,则按以上规律作出的第8个外切正六边形的边长为( )
的第一个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,…,则按以上规律作出的第8个外切正六边形的边长为( )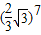
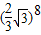
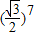

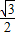 的第一个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,…,则按以上规律作出的第8个外切正六边形的边长为( )
的第一个圆的外切正六边形,接着作上述外切正六边形的外接圆,再作上述外接圆的外切正六边形,…,则按以上规律作出的第8个外切正六边形的边长为( )