题目内容
14、若A(-4,yl),B(-3,y2),C(l,y3)为二次函数y=x2+4x-5的图象上的三点,则yl,y2,y3的大小关系是
y2<y1<y3
.(用<号连接)分析:将二次函数y=x2+4x-5配方,求对称轴,再根据A、B、C三点与对称轴的位置关系,开口方向判断yl,y2,y3的大小.
解答:解:∵y=x2+4x-5=(x+2)2-9,
∴抛物线开口向上,对称轴为x=-2,
∵A、B、C三点中,B点离对称轴最近,C点离对称轴最远,
∴y2<y1<y3.
故本题答案为:y2<y1<y3.
∴抛物线开口向上,对称轴为x=-2,
∵A、B、C三点中,B点离对称轴最近,C点离对称轴最远,
∴y2<y1<y3.
故本题答案为:y2<y1<y3.
点评:本题考查了二次函数的增减性.当二次项系数a>0时,在对称轴的左边,y随x的增大而减小,在对称轴的右边,y随x的增大而增大;a<0时,在对称轴的左边,y随x的增大而增大,在对称轴的右边,y随x的增大而减小.

练习册系列答案
相关题目
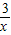 的图象上,则( )
的图象上,则( )