题目内容
若不等式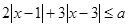
有解，则实数
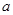最小值是（ ）
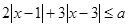有解，则实数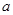最小值是（ ）| A．1 | B．2 | C．4 | D．6 |
C
试题分析：分类讨论：当x＜1或1≤x≤3或x＞3，分别去绝对值解x的不等式，然后根据x对应的取值范围得到a的不等式或不等式组，确定a的范围，最后确定a的最小值．当x＜1，原不等式变为：2-2x+9-3x≤a，解得x≥
∴
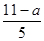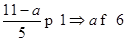当1≤x≤3，原不等式变为：2x-2+9-3x≤a，解得x≥7-a，∴1≤7-a≤3，解得4≤a≤6；当x＞3，原不等式变为：2x-2+3x-9≤a，解得x＜
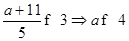综上所述，实数a最小值是4．故选C．点评：本题考查了解含绝对值的一元一次不等式的解法：讨论x的取值范围，然后去绝对值．也考查了不等式和不等式组的解法以及分类讨论思想的运用
练习册系列答案
阅读快车系列答案
相关题目
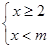有解，那么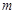
的范围是 . 
（m+4）x|m|﹣3+6＞0是关于x的一元一次不等式，则m= ．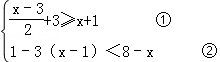
．
．
时，各分母均不为0，
⑤
。
，并写出它的整数解．
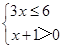的整数解是_________________.