Question

如图，长方形ABCD中，AB=4，AD=3，E是边AB上一点（不与A、B重合），F是边BC上一点（不与B、C重合）．若△DEF和△BEF是相似三角形，则CF=       ．

Answer 1

或．

解析试题分析：①当∠DEF=90°时，设AE=x，则BE=4﹣x，
易求△ADE∽△BEF，
∴，
即，
∵△DEF和△BEF是相似三角形，
∴△DEF和△ADE是相似三角形，
∴或，
∴或，
整理得，6x=12或x²﹣4x+9=0（无解），
解得x=2，
∴BE=4﹣2=2，
，
解得BF=，
CF=3﹣=；
②当∠DFE=90°时，设CF=x，则BF=3﹣x，
易求△BEF∽△CFD，
∴，
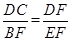即，
∵△DEF和△BEF是相似三角形，
∴△DEF和△DCF是相似三角形，
∴或，
即或，
整理得，8x=12或x²﹣3x+16=0（无解），
解得x=；
综上所述，CF的值为或．
故答案为：或．
故答案是或．
考点：相似三角形的性质．