题目内容
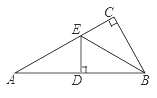
【题目】如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,
(1)求证:AE=BE ;
(2)求AB的长;
(3)若点P是AC上的一个动点,则△BDP周长的最小值=________.
【答案】9+3![]() .
.
【解析】(1)根据平分线的性质和三角形内角和解答即可;(2)根据勾股定理进行解答即可;(3)根据等腰三角形的性质解答即可.
解:(1)∵∠ACB=90°,∠A=30°,∠ABC=90°﹣∠A=60°
∵BE平分∠ABC,∠ABE=30°,
∴∠ABE=∠A,
∴AE=BE.
(2)∵ED⊥AB,∠A=30°,
∴ED=![]() AE=3cm.
AE=3cm.
∴![]() ,
,
∵AE=BE,DE⊥AB.
∴AB=2AD=6![]() .
.
(3)若点P是AC上的一个动点,则△BDP周长的最小值时为△BDP等腰三角形,
可得最小值为:9+3![]() .
.
故答案为:9+3![]() .
.

练习册系列答案
相关题目