题目内容
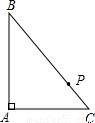
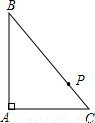
（2005•内江）如图所示，⊙O半径为2，弦BD=2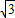
，A为弧BD的中点，E为弦AC的中点，且在BD上，求四边形ABCD的面积．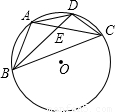
【答案】分析：由A是弧BD的中点，根据垂径定理，可知OF⊥BD，且BF=DF=
BD=
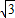，在Rt△BOF中，利用勾股定理，可求出OF=1，即AF=1，那么，S△ABD=
×BD×AF=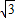
，而E是AC中点，会出现等底同高的三角形，因而有S四边形=2S△ABD=2
．
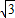解答：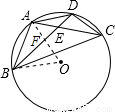
解：连接OA交BD于点F，连接OB，
∵OA在直径上且点A是弧BD中点，
∴OA⊥BD，BF=DF=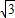
在Rt△BOF中
由勾股定理得OF2=OB2-BF2
OF=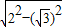
=1
∵OA=2
∴AF=1
∴S△ABD=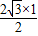
=
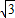
∵点E是AC中点
∴AE=CE
又∵△ADE和△CDE同高
∴S△CDE=S△ADE
∵AE=EC，
∴S△CBE=S△ABE．
∴S△BCD=S△CDE+S△CBE=S△ADE+S△ABE=S△ABD=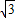
∴S四边形ABCD=S△ABD+S△BCD=2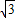
．
点评：本题利用了垂径定理、勾股定理，还有等底同高的三角形面积相等等知识．
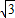BD=，在Rt△BOF中，利用勾股定理，可求出OF=1，即AF=1，那么，S△ABD=×BD×AF=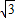，而E是AC中点，会出现等底同高的三角形，因而有S四边形=2S△ABD=2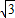．解答：
解：连接OA交BD于点F，连接OB，∵OA在直径上且点A是弧BD中点，
∴OA⊥BD，BF=DF=
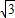
在Rt△BOF中
由勾股定理得OF2=OB2-BF2
OF=
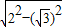=1∵OA=2
∴AF=1
∴S△ABD=
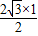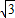
=∵点E是AC中点
∴AE=CE
又∵△ADE和△CDE同高
∴S△CDE=S△ADE
∵AE=EC，
∴S△CBE=S△ABE．
∴S△BCD=S△CDE+S△CBE=S△ADE+S△ABE=S△ABD=
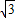
∴S四边形ABCD=S△ABD+S△BCD=2
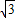．点评：本题利用了垂径定理、勾股定理，还有等底同高的三角形面积相等等知识．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
