题目内容
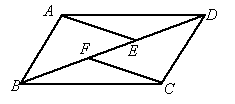
在?ABCD中，对角线AC和BD相交于点O，如果AC=10，BD=12，AB=m，那么m的取值范围是
- A.2＜m＜22
- B.1＜m＜11
- C.10＜m＜12
- D.5＜m＜6
B
分析：根据平行四边形的性质求出OA、OB，根据三角形的三边关系定理得到OB-OA＜m＜OA+OB，代入求出即可．
解答：
解：∵四边形ABCD是平行四边形，AC=10，BD=12，
∴OA=OC=5，OD=OB=6，
在△OAB中，OB-OA＜m＜OA+OB，
∴6-5＜m＜6+5，
∴1＜m＜11．
故选B．
点评：本题考查对平行四边形的性质，三角形的三边关系定理等知识点的理解和掌握，求出OA、OB后得出OB-OA＜m＜OA+OB是解此题的关键．
分析：根据平行四边形的性质求出OA、OB，根据三角形的三边关系定理得到OB-OA＜m＜OA+OB，代入求出即可．
解答：
解：∵四边形ABCD是平行四边形，AC=10，BD=12，∴OA=OC=5，OD=OB=6，
在△OAB中，OB-OA＜m＜OA+OB，
∴6-5＜m＜6+5，
∴1＜m＜11．
故选B．
点评：本题考查对平行四边形的性质，三角形的三边关系定理等知识点的理解和掌握，求出OA、OB后得出OB-OA＜m＜OA+OB是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
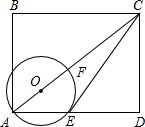=∠DCE．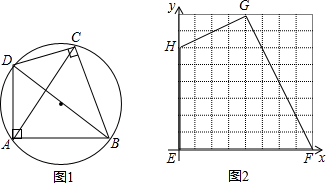
在下面推理过程的括号内填上推理的依据
、∠B＋∠C＝
时，边AB与CD的关系是________．
ABCD中，∠BAC＝
，∠BCA＝
，则∠B＝________．