题目内容
9、已知C是以AB为直径的⊙O上一点,过点C作⊙O的切线交直线AB于点D,则当△ACD为等腰三解形时,∠ACD的度数为
30°或120°
.分析:
如图,连接OC,BC.
点C的位置有两种情况,
①为左图时,AC=CD;
②右上图.AD=AC.
根据切线的性质和三角形内角和定理分别求解.

如图,连接OC,BC.
点C的位置有两种情况,
①为左图时,AC=CD;
②右上图.AD=AC.
根据切线的性质和三角形内角和定理分别求解.
解答: 解:
解:
如图,连接OC,BC.
AB是直径,则有∠ACB=90°;CD是切线,C是切点,有∠OCD=90°;则点C的位置有两种情况:
①为左图时,AC=CD,OC=OA,
∴∠D=∠A=∠ACO,∠COD=2∠A=2∠D.
∵∠COD+∠D=2∠D+∠D=90°,
∴∠ACO=∠D=30°,∠ACD=∠OCD+∠ACO=120°.
②右上图.∵AD=AC,
∴∠D=∠DCA;
由弦切角定理知,∠DCA=∠B;
∴∠D+∠B+∠DCA+∠ACB=3∠DCA+90°=180°,
∴∠ACD=30°.
∴∠ACD的度数为120°或30°.
 解:
解:如图,连接OC,BC.
AB是直径,则有∠ACB=90°;CD是切线,C是切点,有∠OCD=90°;则点C的位置有两种情况:
①为左图时,AC=CD,OC=OA,
∴∠D=∠A=∠ACO,∠COD=2∠A=2∠D.
∵∠COD+∠D=2∠D+∠D=90°,
∴∠ACO=∠D=30°,∠ACD=∠OCD+∠ACO=120°.
②右上图.∵AD=AC,
∴∠D=∠DCA;
由弦切角定理知,∠DCA=∠B;
∴∠D+∠B+∠DCA+∠ACB=3∠DCA+90°=180°,
∴∠ACD=30°.
∴∠ACD的度数为120°或30°.
点评:本题利用了切线的性质,直径对的圆周角是直角,等边对等角,三角形内角和定理求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
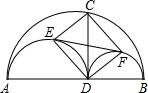 半圆,EF是这两个半圆的外公切线,E、F为切点.
半圆,EF是这两个半圆的外公切线,E、F为切点. 半圆,EF是这两个半圆的外公切线,E、F为切点.
半圆,EF是这两个半圆的外公切线,E、F为切点.
