题目内容
【题目】如图是一块地的平面图,AD=4m,CD=3m,AB=13m,BC=12m,∠ADC=90°,求这块地的面积. 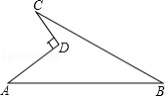
【答案】解:如图,连接AC, ∵AD=4,CD=3,∠ADC=90°,
∴AC= ![]() =5,
=5,
∴S△ACD=6,
在△ABC中,∵AC=5,BC=12,AB=13,
∴AC2+BC2=AB2 ,
∴△ABC为直角三角形,且∠ACB=90°,
∴Rt△ABC的面积=30,
∴四边形ABCD的面积=30﹣6=24.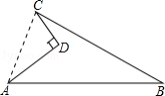
【解析】连接AC,根据解直角△ADC求AC,求证△ACB为直角三角形,根据四边形ABCD的面积=△ABC面积﹣△ACD面积即可计算.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目