题目内容
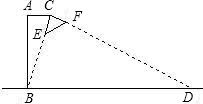
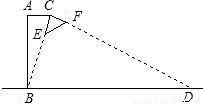
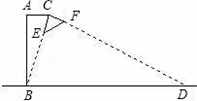
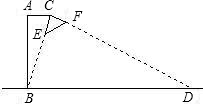如图所示为某种型号的台灯的横截面图，已知台灯灯柱AB长30cm，且与水平桌面垂直，灯臂AC长为15cm，灯头的横截面△CEF为直角三角形，当灯臂AC与灯柱AB垂直时，沿CE边射出的光线刚好射到底座B点，若不考虑其它因素，该台灯在桌面可照亮的宽度BD的长为分析：此题是一道实际问题，根据题意可证明出△ABC∽△CDB，利用相似三角形的性质解答．
解答：解：∵AB⊥BD，AC⊥AB，
∴AC∥BD．
∴∠ACB=∠DBC．
∵∠A=∠BCD=90°，
∴△ABC∽△CDB．
∴
=
．
∴BC2=AC•BD．
在Rt△ABC中，BC2=AC2+AB2=152+302=1125，
∴15BD=1125．
∴BD=75（cm）．
∴AC∥BD．
∴∠ACB=∠DBC．
∵∠A=∠BCD=90°，
∴△ABC∽△CDB．
∴
| AC |
| BC |
| BC |
| BD |
∴BC2=AC•BD．
在Rt△ABC中，BC2=AC2+AB2=152+302=1125，
∴15BD=1125．
∴BD=75（cm）．
点评：本题只要是把实际问题抽象到相似三角形中，利用相似三角形的相似比，列出方程，通过解方程求出BD的长度．
练习册系列答案
名校课堂系列答案
相关题目
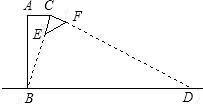如图所示为某种型号的台灯的横截面图，已知台灯灯柱AB长30cm，且与水平桌面垂直，灯臂AC长为15cm，灯头的横截面△CEF为直角三角形，当灯臂AC与灯柱AB垂直时，沿CE边射出的光线刚好射到底座B点，若不考虑其它因素，该台灯在桌面可照亮的宽度BD的长为________cm．
