Question

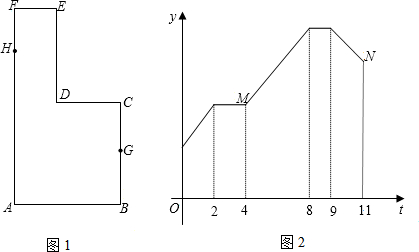
已知动点P以每秒2cm的速度沿如图甲所示的边框按B→C→D→E→F→A的路径移动，相应的△ABP的面积S关于时间t的函数图象如图乙，若AB=6，则图乙中a、b的值正确的为（　　）

A．a=24，b=17

B．a=24，b=19

C．a=22，b=14

D．a=20，b=19

Answer 1

分析：根据函数图象知道动点p从B点到C点的运动得到的三角形的最大面积是24，据此求得a的值，再求出点P从B点到A点移动的总路程，最后根据点P移动的速度求出所用的时间，即可得出b的值．

解答：解：∵P以每秒2cm的速度沿如图甲所示的边框按B→C→D→E→F→A的路径移动，
∴BC=2×4=8cm，AB=6cm，DC=2×2=4cm，DE=2×3=6cm，
∴△ABP的面积S=

1

2

×6×8=24（cm）²，EF=AB-CD=6-4=2cm，AF=BC+DE=8+6=14cm，
∴a=24，
b=

BC+CD+DE+EF+FA

2

=

8+4+6+2+14

2

=

34

2

=17．
故选A．

点评：本题考查了动点问题的函数图象，本题需结合两个图，得到相应的线段长度，进而求解．