题目内容
已知:如图,矩形ABCD中,CD=2,AD=3,以C点为圆心,作一个动圆,与线段AD交于点P(P和A、D不重合),过P作⊙C的切线交线段AB于F点.
(1)求证:△CDP∽△PAF;
(2)设DP=x,AF=y,求y关于x的函数关系式,及自变量x的取值范围;
(3)是否存在这样的点P,使△APF沿PF翻折后,点A落在BC上,请说明理由.(本题12分)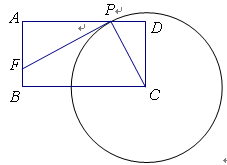
(1)见解析(2)y= (0<x<3)(3)不存在符合要求的点P
(0<x<3)(3)不存在符合要求的点P
解析试题分析:(1)∵PF切⊙C于点P,∴CP⊥PF………………………………………………(1分)
∴∠1+∠2=90º,而矩形ABCD中,∠A=∠D=90º,∴∠2+∠3=90º,∴∠1=∠3,∴△CDP∽△PAF……………………………(4分)
(2)∴ =
= ,即
,即 =
= ,整理可得,y=
,整理可得,y= (0<x<3)8′
(0<x<3)8′
(3)假设点A的落点为A’,则AA’⊥PF,AF=A’F
∴AA’∥PC,得□AA’CP,则A’B=DP
在Rt△A’BF中,x2+(2-y)2=y2,……………………………………………12′
即3x2-6x+4=0,该方程无实数根,不存在符合要求的点P…(8分)
考点:本题考查了矩形性质定理;函数
点评:此类试题属于难度很大的综合性试题,考生解答此类试题时一定要掌握好每一个小知识点

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF.
已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF. 19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE.
19、已知,如图,矩形ABCD中,E是CD的中点,连接BE并延长BE交AD的延长线于点F,连接AE. 上,AH=2,连接CF.
上,AH=2,连接CF. 已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF.
已知:如图,矩形ABCD中,点E在边AB上,∠DEB的平分线EF交BC的延长线于点F,且AB=BF,连接DF. (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.